
【题目】如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.求证:
(1)BE=CF;
(2)四边形BECF是平行四边形.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD的四边都相等,等边△AEF的顶点E、F分别在BC、CD上,且AE=AB,则∠C=( )

A. 100° B. 105° C. 110° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一根24cm的筷子置于底面直径为8cm,高为15cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC 的外接圆,AB=AC,BD是⊙O的直径,PA∥BC,与DB的延长线交于点P,连接AD.
(1)求证:PA是⊙O的切线;
(2)若AB= ![]() ,BC=4,求AD的长.
,BC=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.
(1)﹣7+(﹣8)﹣(﹣18)﹣13
(2)(﹣1)3×(﹣5)﹣(﹣3)÷(﹣![]() )
)
(3)(![]() -
-![]() -
-![]() )÷(﹣
)÷(﹣![]() )
)
(4)﹣12018﹣2![]() ×[13﹣(﹣5)2]
×[13﹣(﹣5)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
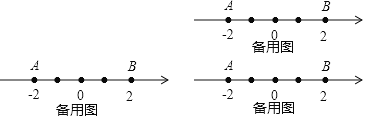
【题目】已知数轴上两点A、B,其中A表示的数为-2,B表示的数为2,若在数轴上存在一点C,使得AC+BC=n,则称点C叫做点A、B的“n节点”.例如图1所示:若点C表示的数为0,有AC+BC=2+2=4,则称点C为点A、B的“4节点”.
请根据上述规定回答下列问题:
(1)若点C为点A、B的“n节点”,且点C在数轴上表示的数为-4,求n的值;
(2)若点D是数轴上点A、B的“5节点”,请你直接写出点D表示的数为______;
(3)若点E在数轴上(不与A、B重合),满足BE=![]() AE,且此时点E为点A、B的“n节点”,求n的值.
AE,且此时点E为点A、B的“n节点”,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A在O正北方向,B在O正东方向,且A、B到点O的距离相等,甲从A出发,以每小时60千米的速度朝正东方向行驶,乙从B出发,以每小时40千米的速度朝正北方向行驶,1小时后,位于点O处的观察员发现甲乙两人之间的夹角为45°,此时甲乙两人相距( )千米。

A. 80 B. 50![]() C. 100
C. 100![]() D. 100
D. 100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高居民的节水意识,向阳小区开展了“建设节水型社区,保障用水安全”为主题的节水宣传活动,小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查,她在300户家庭中,随机调查了50户家庭5月份的用水量情况,结果如图所示.

(1)试估计该小区5月份用水量不高于12 t的户数占小区总户数的百分比;
(2)把图中每组用水量的值用该组的中间值(如0~6的中间值为3)来替代,估计该小区5月份的用水量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com