
【题目】
(发现)如图①,在△ABC中,点D,E分别是AB,AC的中点,可以得到:DE∥BC,且DE=![]() BC.(不需要证明)
BC.(不需要证明)

(探究)如图②,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,判断四边形EFGH的形状,并加以证明.
(应用)在(探究)的条件下,四边形ABCD中,满足什么条件时,四边形EFGH是菱形?你添加的条件是: .(只添加一个条件)
【答案】(1)见解析;(2)AC=BD.
【解析】
探究:连结AC,由四个中点可得EF∥AC且EF=![]() AC、GH∥AC且GH=
AC、GH∥AC且GH=![]() AC,据此可得EF∥GH,且EF=GH,从而得证;
AC,据此可得EF∥GH,且EF=GH,从而得证;
应用:添加AC=BD,连接BD,由EF=![]() AC、EH=
AC、EH=![]() BD,且AC=BD知EF=EH,根据四边形EFGH是平行四边形即可得证;
BD,且AC=BD知EF=EH,根据四边形EFGH是平行四边形即可得证;
探究:平行四边形,
证明:连结AC,
∵E、F分别是AB、BC的中点,
∴EF∥AC,且EF=![]() AC.
AC.
∵G、H分别是CD、AD的中点,
∴GH∥AC,且GH=![]() AC.
AC.
∴EF∥GH,且EF=GH.
∴四边形EFGH是平行四边形.
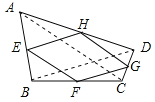
应用:
AC=BD;
连接BD,
∵EF=![]() AC、EH=
AC、EH=![]() BD,且AC=BD,
BD,且AC=BD,
∴EF=EH,
又∵四边形EFGH是平行四边形,
∴四边形EFGH是菱形.
故答案为:AC=BD.


科目:初中数学 来源: 题型:
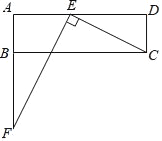
【题目】如图,在矩形ABCD中,已知 AD>AB.在边AD上取点E,连结CE.过点E作EF⊥CE,与边AB的延长线交于点F.
(1)证明:△AEF∽△DCE.
(2)若AB=4,AE=6,AD=14,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是 2019 年五月的月历,“T”型、“田”型两个阴影图形分别覆盖其中四个方格(可以重叠覆盖),设“T”型阴影覆盖的最小数字为 a,四个数字之和为 S1,“田”型阴影覆盖的最小数字为 b,四个数字之和为 S2.
(1) S1 的值能否为 50?若能,求 a 的值;若不能,说明理由;
(2)S1+ S2 值能否为 35,若能,求 a,b 的值;若不能,说明理由;
(3)若 S1+ S2=43,求 S1-S2 的值为 (直接写结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价40元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠两盒乒乓球;乙店的优惠办法是:全部商品按定价的8.5折出售.某班需购买乒乓球拍4副,乒乓球若干盒(不少于8盒).


(1)当购买乒乓球的盒数为x盒时,在甲店购买需付款 元?在乙店购买需付款 元?(用含x的代数式表示)
(2)当购买乒乓球盒数为20盒时,去哪一家商店购买较合算?请计算说明.
(3) 当购买乒乓球盒数为20盒时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点示数
点示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() .
.
![]()
(1)![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
(2)若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合;
(3)点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,同时,点
个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动,假设
个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,那么
,那么![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们自从有了用字母表示数,发现表达有关的数和数量关系更加简洁明了,从而更助于我们发现更多有趣的结论,请你按要求试一试。
(1)用代数式表示:
①![]() 与
与![]() 的差的平方;②
的差的平方;②![]() 、
、![]() 两数的平方和与
两数的平方和与![]() ,
,![]() 两数积的2倍的差;
两数积的2倍的差;
(2)当![]() =3,
=3,![]() =-2时,求第(1)题中①②所列的代数式的值;
=-2时,求第(1)题中①②所列的代数式的值;
(3)由第(2)题的结果,你发现了什么等式?
(4)利用你发现的结论:求20182-2×2018×2017+20172的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
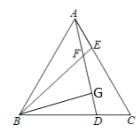
【题目】如图,△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F,BG⊥AD,垂足为G.
(1)求证:AD=BE;
(2)求∠AFB的度数;
(3)线段FG与BF有什么数量关系?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com