
【题目】已知,如图,AB 是⊙O 的直径,CD 是弦,CD⊥AB 于点 E,点 G 在直径 DF 的延 长线上,∠D=∠G=30°.
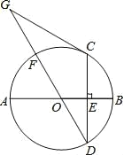
(1)求证:CG 是⊙O 的切线;
(2)若 CD=6,求 GF 的长.
【答案】(1)见解析;(2)2![]()
【解析】
(1)连接OC,利用半径相等及三角形内角和定理计算出∠GCO =90°即可.
(2)利用30度角所对直角边等于斜边一半,设![]() ,则
,则![]() ,利用勾股定理构建方程求出半径,在直角三角形OCG中利用先是关系即可求得答案.
,利用勾股定理构建方程求出半径,在直角三角形OCG中利用先是关系即可求得答案.
(1)证明:连接OC,如图:
∵OC=OD,∠D=30°,
∴∠OCD=∠D=30°.
∵∠G=30°,
∴∠DCG=180°﹣∠D﹣∠G=120°.
∴∠GCO=∠DCG﹣∠OCD=90°.
∴OC⊥CG.
又∵OC是⊙O的半径.
∴CG是⊙O的切线.
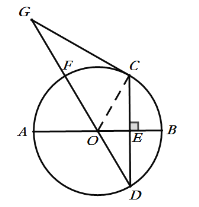
(2)解:∵AB是⊙O的直径,CD⊥AB,
∴CE=![]() CD=3.
CD=3.
∵在Rt△OCE中,∠CEO=90°,∠OCE=30°,
∴EO=![]() CO,CO2=EO2+CE2.
CO,CO2=EO2+CE2.
设EO=x,则CO=2x.∴(2x)2=x2+32.
解之得x=![]() (舍负值).
(舍负值).
∴CO=2![]() .
.
∴FO=2![]() .
.
在△OCG中,∵∠OCG=90°,∠G=30°,
∴GO=2CO=4![]() .
.
∴GF=GO﹣FO=2![]()


科目:初中数学 来源: 题型:
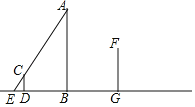
【题目】如图,夜晚,小华利用路灯A测量建筑物GF的高度,他在点D处竖立了一根木杆CD,测得木杆CD的影长DE=1.5m,AB⊥EG,CD⊥EG,GF⊥EG.
(1)在图中画出表示建筑物GF影子的线段GH;
(2)已知木杆的高CD=2m,建筑物GF的影子GH=7.8m,木杆CD与路灯杆AB之间的距离BD=5.85m,路灯杆AB与建筑物GF之间的距离BG=6.9m,请你根据题中提供的相关信息,求出建筑物GF的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
![]() 根据上表填空:
根据上表填空:
①抛物线与![]() 轴的交点坐标是________和________;
轴的交点坐标是________和________;
②抛物线经过点![]() ,________
,________![]() ;
;
③在对称轴右侧,![]() 随
随![]() 增大而________;
增大而________;
![]() 试确定抛物线
试确定抛物线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E,F分别为边AB和CD的中点,连接DE,BF,且AB=2AD=4.
(1)求证:△AED≌△CFB;
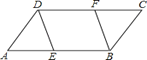
(2)当四边形DEBF为菱形时,求出该菱形的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).
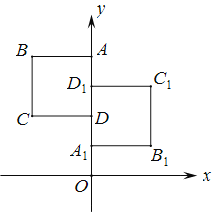
(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
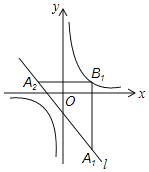
【题目】如图,在平面直角坐标系xOy中,已知直线l:y=﹣x﹣1,双曲线y=![]() ,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2018=_____;若要将上述操作无限次地进行下去,则a1不可能取的值是_____.
,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2018=_____;若要将上述操作无限次地进行下去,则a1不可能取的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=![]() x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳![]() x2元的附加费,设月利润为w外(元).
x2元的附加费,设月利润为w外(元).
(1)当x=1000时,y= 元/件,w内= 元;
(2)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各数位上的字互不相同,且都不为零,那么称这个数为“相异数”.将一个“相异数”任意两个数位上的字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为![]() .例如
.例如![]() ,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的好得到132,这三个新三位数的和为
,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的好得到132,这三个新三位数的和为![]() ,
,![]() ,所以
,所以![]() .
.
(1)计算:![]() ,
,![]() ;
;
(2)若s,t都是“相异数”,其中![]() ,
,![]() (
(![]() ,
,![]() ,x,y都是正整数),规定:
,x,y都是正整数),规定:![]() ,当
,当![]() 时,求k的最大值.
时,求k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
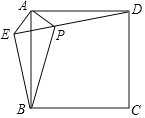
【题目】如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=2,PB=2![]() .则正方形ABCD的面积是_____.
.则正方形ABCD的面积是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com