
分析 (1)将x=1000代入函数关系式求得y,并根据等量关系“利润=销售额-成本-广告费”求得w内;
(2)根据等量关系“利润=销售额-成本-广告费”“利润=销售额-成本-附加费”列出两个函数关系式;
(3)对w内函数的函数关系式求得最大值,再求出w外的最大值并令二者相等求得a值;
(4)通过对国内和国外的利润比较,又由于a值不确定,故要讨论a的取值范围.
解答 解:(1)x=1000,y=$-\frac{1}{100}$×1000+150=140,
w内=(140-20)×1000-62500=57500.
故答案为:140;57500.
(2)w内=x(y-20)-62500=$-\frac{1}{100}$x2+130x-62500,
w外=$-\frac{1}{100}$x2+(150-a)x.
(3)当x=$-\frac{130}{2×(-\frac{1}{100})}$=6500时,w内最大;
由题意在国外销售月利润的最大值与在国内销售月利润的最大值相同,得:$\frac{0-(150-a)^{2}}{4×(-\frac{1}{100})}$=$\frac{4×(-\frac{1}{100})×(-62500)-13{0}^{2}}{4×(-\frac{1}{100})}$,
解得a1=30,a2=270(不合题意,舍去).
∴a=30.
(4)当x=5000时,w内=337500,w外=-5000a+500000.
若w内<w外,则a<32.5;
若w内=w外,则a=32.5;
若w内>w外,则a>32.5.
∴当10≤a<32.5时,选择在国外销售;当a=32.5时,在国外和国内销售都一样;当32.5<a≤40时,选择在国内销售.
点评 本题考查了二次函数在实际生活中的应用,考查了一次函数的应用,根据题意求得函数解析式是解题的关键.


科目:初中数学 来源: 题型:解答题
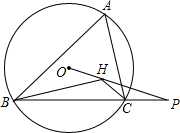 如图所示,已知锐角△ABC的外接圆半径R=1,∠BAC=60°,△ABC的垂心和外心分别为H、O,连接OH、BC交于点P
如图所示,已知锐角△ABC的外接圆半径R=1,∠BAC=60°,△ABC的垂心和外心分别为H、O,连接OH、BC交于点P查看答案和解析>>
科目:初中数学 来源: 题型:解答题
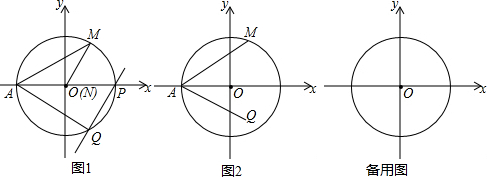
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
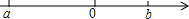 若有理数a,b在数轴上对应的点如图所示,则a、b、-a、-b的大小关系是( )
若有理数a,b在数轴上对应的点如图所示,则a、b、-a、-b的大小关系是( )| A. | a<b<-a<-b | B. | a<-b<b<-a | C. | -b<a<b<-a | D. | -a<-b<a<b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com