
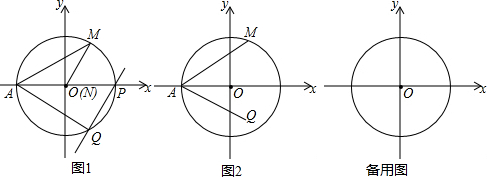
分析 (1)如图1,根据圆周角定理可求出∠MAP、∠AQP,再根据∠MAQ可依次求出∠PAQ,∠APQ;
(2)连接MQ,交x轴于E,连接PQ,交x轴于F,连接PM,如图2,由题可得:△MAQ和△MNP均为等边三角形,由此可证到△AMN≌△QMP,则有∠MAN=∠MQP.根据三角形外角的性质可得到∠MAN+∠AMQ=∠AEQ=∠MQP+∠AFQ,从而可得到∠AFQ=∠AMQ=60°(即α=60°);
(3)连接MQ,交x轴于E,连接PQ,交x轴于F,连接PM,MF,OM,过点M作MH⊥x轴于H,设PQ与⊙O相切于点G,连接OG,如图3①、图3②.则有∠OGF=90°.由(2)可得∠AFQ=∠AMQ=60°,由此可得A、M、F、Q四点共圆,根据圆周角定理可得∠AFM=∠AQM=60°.在Rt△OGF中运用三角函数可求得OF=$\frac{2\sqrt{3}}{3}$,在Rt△MHF中运用三角函数可得$\frac{MH}{HF}$=$\sqrt{3}$.设HF=x,则MH=$\sqrt{3}$x,OH=$\frac{2\sqrt{3}}{3}$-x.在Rt△OHM中运用勾股定理可求出x,从而可得OH,MH,就可得到点M的坐标.
解答 解:(1)如图1,
∵∠MOP=60°,∴∠MAP=30°.
∵∠MAQ=60°,∴∠QAP=30°.
∵AP是⊙O的直径,
∴∠AQP=90°,
∴∠APQ=60°,即α=60°.
故答案为60;
(2)连接MQ,交x轴于E,连接PQ,交x轴于F,连接PM,如图2.
由题可得:△MAQ和△MNP均为等边三角形,
∴MA=MQ,MN=MP,∠AMQ=∠NMP=60°,
∴∠AMN=∠QMP.
在△AMN和△QMP中,
$\left\{\begin{array}{l}{MA=MQ}\\{∠AMN=∠QMP}\\{MQ=MP}\end{array}\right.$,
∴△AMN≌△QMP,
∴∠MAN=∠MQP.
∵∠AEQ=∠MAN+∠AMQ,∠AEQ=∠MQP+∠AFQ,
∴∠AFQ=∠AMQ=60°,
∴α的度数为60°;
(3)连接MQ,交x轴于E,连接PQ,交x轴于F,连接PM,MF,OM,
过点M作MH⊥x轴于H,设PQ与⊙O相切于点G,连接OG,如图3①、图3②.
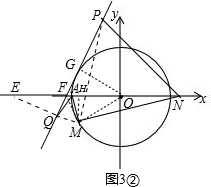
则有∠OGF=90°.
由(2)可得∠AFQ=∠AMQ=60°,
∴A、M、F、Q四点共圆,
∴∠AFM=∠AQM=60°.
∴在Rt△MHF中,tan∠HFM=$\frac{MH}{HF}$=$\sqrt{3}$.
在Rt△OGF中,sin∠OFG=$\frac{OG}{OF}$=$\frac{\sqrt{3}}{2}$,
∵OG=1,∴OF=$\frac{2\sqrt{3}}{3}$.
设HF=x,则MH=$\sqrt{3}$x,OH=$\frac{2\sqrt{3}}{3}$-x.
在Rt△OHM中,由勾股定理可得:
($\frac{2\sqrt{3}}{3}$-x)2+($\sqrt{3}$x)2=12,
解得x1=x2=$\frac{\sqrt{3}}{6}$,
∴OH=$\frac{2\sqrt{3}}{3}$-$\frac{\sqrt{3}}{6}$=$\frac{\sqrt{3}}{2}$,MH=$\frac{1}{2}$,
∴点M的坐标为($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)或(-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
故答案为($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)或(-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
点评 本题主要考查了圆周角定理、切线的性质、四点共圆的判定、等边三角形的判定与性质、特殊角的三角函数值、勾股定理等知识,在△OMF中求出OF及∠OFM是解决第(3)小题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
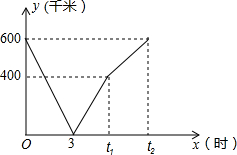 一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系,则t2-t1的值为2.5小时.
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系,则t2-t1的值为2.5小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
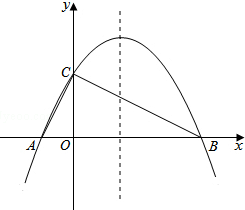 如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
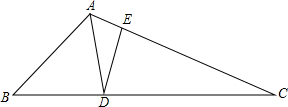 如图,已知△ABC,AD平分∠BAC,DE垂直AC,垂足为E,∠ADB=2∠B=4∠C,AE=$\frac{3}{4}$,CD=$\frac{7}{2}$,则线段AB=$\frac{55}{26}$.
如图,已知△ABC,AD平分∠BAC,DE垂直AC,垂足为E,∠ADB=2∠B=4∠C,AE=$\frac{3}{4}$,CD=$\frac{7}{2}$,则线段AB=$\frac{55}{26}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.133×104万 | B. | 1.33×103万 | C. | 1.33×104万 | D. | 13.3×102万 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com