【题目】如图，在平面直角坐标系中，已知直线y=kx+6与x轴、y轴分别交于A、B两点，且△ABO的面积为12．

（1）求k的值；
（2）若点P为直线AB的一动点，P点运动到什么位置时，△PAO使以OA为底的等腰三角形？求出此时点P的坐标；
（3）在（2）的条件下，坐标平面内是否存在点M，使以P、B、O、M为顶点组成的平行四边形为菱形？若存在，求出点M坐标；若不存在，试说明理由．

参考答案：

【答案】
（1）解：∵y=kx+b，

∴B（0，6），

∴OB=6．

∵S△ABO=12，

∴ 6OA=12，

∴OA=4，

∴A（﹣4，0），

把A（﹣4，0）代入y=kx+6，可得k= ．


（2）解：∵△PAO使以OA为底的等腰三角形，

∴PA=PO，

∴∠PAO=∠POA，

∵∠PAO+∠ABO=90°，∠POA+∠POB=90°，

∴∠PBO=∠POB，

∴PB=PO，

∴PA=PB，

∵A（﹣4，0），B（0，6），

∴P（﹣2，3）．


（3）解：存在．

①如图1中，当四边形PBMO是平行四边形时，

∵PB=PO，

∴四边形PBMO是菱形，易知P、M关于y轴对称，

∴M（2，3）．

②如图2中，当四边形PBOM是平行四边形时，

∵PB≠OB，

∴平行四边形PBMO表示菱形．

③如图3中，当四边形OPMB是平行四边形时，

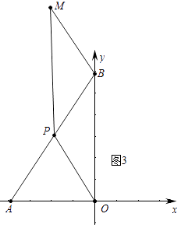
∵OP≠OB，

∴四边形OPMB表示菱形．

综上所述，满足条件的点M的坐标为（2，3）．


【解析】（1）利用三角形的面积公式求出点A的坐标即可，利用待定系数法解决问题；（2）当△PAO使以OA为底的等腰三角形时，P是AB的中点，利用中点坐标公式即可解决问题；（3）分三种情形讨论即可解决问题；

关闭