
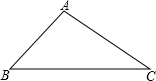
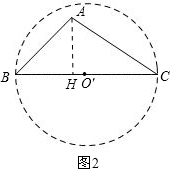
 某公司临街的外墙上有一块三角形的墙面(如图所示)发生破损现象,公司领导让工人师傅做一个圆形广告牌,将破损面全部覆盖住,工人师傅量的∠B=45°,∠C=30°,AB=4m,考虑到成本问题,应使所做的广告牌尽可能小,同学晓敏认为,作△ABC的外接圆,即可能得到满足要求的广告牌.
某公司临街的外墙上有一块三角形的墙面(如图所示)发生破损现象,公司领导让工人师傅做一个圆形广告牌,将破损面全部覆盖住,工人师傅量的∠B=45°,∠C=30°,AB=4m,考虑到成本问题,应使所做的广告牌尽可能小,同学晓敏认为,作△ABC的外接圆,即可能得到满足要求的广告牌. 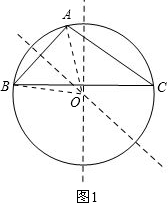
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| AH |
| HC |
| 2 |
| 6 |
| 2 |
| 6 |
| 2 |
| 6 |
| 2 |
| 6 |
| 3 |
| 3 |
| 3 |
| 3 |


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,点A、B的坐标分别为(-1,3)、(-4,1),先将线段AB沿一确定方向平移得到线段A1B1,点A的对应点为A1,点B1的坐标为(0,2),在将线段A1B1绕原点O顺时针旋转90°得到线段A2B2,点A1的对应点为点A2.
如图,在平面直角坐标系中,点A、B的坐标分别为(-1,3)、(-4,1),先将线段AB沿一确定方向平移得到线段A1B1,点A的对应点为A1,点B1的坐标为(0,2),在将线段A1B1绕原点O顺时针旋转90°得到线段A2B2,点A1的对应点为点A2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com