
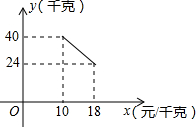
 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:分析 (1)由图象可知y与x之间是一次函数关系,可设y=kx+b,把(10,40),(18,24)代入可得;
(2)根据:销售利润W=该产品每千克利润×销售量,列出函数关系式,配成二次函数顶点式,结合自变量取值范围可得其最值.
解答 解:(1)设y与x之间的函数关系式:y=kx+b,
把(10,40),(18,24)代入得:
$\left\{\begin{array}{l}{10k+b=40}\\{18k+b=24}\end{array}\right.$,
解得:$\left\{\begin{array}{l}k=-2\\ b=60\end{array}\right.$,
∴y与x之间的函数关系式y=-2x+60(10≤x≤18);
(2)W=(x-10)(-2x+60)
=-2x2+80x-600
=-2(x-20)2+200,
∴当x<20时,w随着x的增大而增大,
∵10≤x≤18,
∴当x=18时,W最大,最大为192.
即当销售价为18元时,每天的销售利润最大,最大利润是192元.
点评 本题主要考查二次函数的应用能力,结合函数图象待定系数法求函数解析式是基本能力,确定利润最大值通常利用二次函数来解决,根据题意找到相等关系列出函数解析式是解题关键.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:解答题
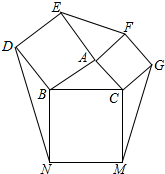 如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN
如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com