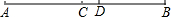练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．如图，C是线段AB的中点，D在线段CB上，AD=6，DB=4，则CD的长等于1．

    分析 先根据C是线段AB的中点得出BC的长，再由CD=BC-BD即可得出结论．

    解答 解：∵C是线段AB的中点，AD=6，DB=4，
    ∴BC=$\frac{1}{2}$（AD+DB）=5，
    ∴CD=BC-BD=5-4=1．
    故答案为：1．

    点评 本题考查的是两点间的距离，熟知各线段之间的和、差及倍数关系是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．A，B两个港口相距300公里．若甲船顺水自A港口驶向B港口，乙船同时逆水驶向A港口，两船在C处相遇，若乙船自A港口驶向B港口，同时甲船自B港口驶向A港口，则两船在D处相遇，C处与D处相距30公里，已知甲船的速度为27km/h．请解答下列问题：
    （1）若水流的速度为2km/h，求乙船的速度．
    （2）若不知水流的速度，只知乙船的速度比甲船的速度大，你还能求出乙船的速度吗？若能，请求出来；若不能，请简要说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如果a表示一个负数，则|a|等于（　　）
    A．aB．0C．-aD．不确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

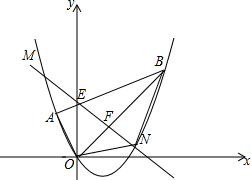    15．如图，平面直角坐标系xOy中点A的坐标为（-1，1），点B的坐标为（3，3），抛物线经过A、O、B三点，连接OA、OB、AB，线段AB交y轴于点E．
    （1）求点E的坐标；
    （2）求抛物线的函数解析式；
    （3）点F为线段OB上的一个动点（不与点O、B重合），直线EF与抛物线交于M、N两点（点N在y轴右侧），连接ON、BN，当四边形ABNO的面积最大时，求点N的坐标并求出四边形ABNO面积的最大值；
    （4）在（3）的条件下，当四边形ABNO面积最大时，在抛物线上是否存在点P，使得∠PAO=∠NEO？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列运算正确的是（　　）
    A．$\sqrt{9}=±3$B．（-2）3=8C．-|-3|=3D．-22=-4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图是按规律排列的式子，若第六行最中间两项的和的值是2052，则a的值为±2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．定义一种新运算?：a?b=4a+b，试根据条件回答问题
    （1）计算：2?（-3）=5；
    （2）若x?（-6）=3?x，请求出x的值；
    （3）这种新定义的运算是否满足交换律，若不满足请举一个反例，若满足，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

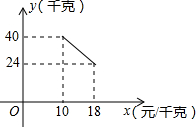    16．某经销商销售一种产品，这种产品的成本价为10元/千克，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于18元/千克，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）之间的函数关系如图所示：
    （1）求y与x之间的函数关系式，并写出自变量x的取值范围；
    （2）求每天的销售利润W（元）与销售价x（元/千克）之间的函数关系式；若你是商场负责人，会将销售价定为多少，来保证每天的销售利润最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，△ABC中，MN∥BC，MC与BN相交于点O，如果AM：MB=1：2，则NO：OB=（　　）
    A．1：2B．1：3C．1：4D．2：3

    查看答案和解析>>

    同步练习册答案