
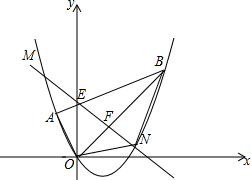
 ÈçÍŒŁŹÆœĂæÖ±œÇŚű±êÏ”xOyÖĐ”ăA”ÄŚű±êÎȘŁš-1ŁŹ1Ł©ŁŹ”ăB”ÄŚű±êÎȘŁš3ŁŹ3Ł©ŁŹĆŚÎïÏߟčęAĄąOĄąBÈę”㣏ÁŹœÓOAĄąOBĄąABŁŹÏ߶ÎABœ»yÖáÓÚ”ăEŁź
ÈçÍŒŁŹÆœĂæÖ±œÇŚű±êÏ”xOyÖĐ”ăA”ÄŚű±êÎȘŁš-1ŁŹ1Ł©ŁŹ”ăB”ÄŚű±êÎȘŁš3ŁŹ3Ł©ŁŹĆŚÎïÏߟčęAĄąOĄąBÈę”㣏ÁŹœÓOAĄąOBĄąABŁŹÏ߶ÎABœ»yÖáÓÚ”ăEŁź·ÖÎö Łš1Ł©ÏÈÀûÓĂŽę¶šÏ”Êę·šÇółöÖ±ÏßAB”ÄœâÎöÊœŁŹÈ»șóŒÆËăŚÔ±äÁżÎȘ0ʱ”ÄșŻÊęÖ”ŒŽżÉ”Ă”œE”ăŚű±êŁ»
Łš2Ł©ÀûÓĂŽę¶šÏ”ÊęÇóĆŚÎïÏߔĜâÎöÊœŁ»
Łš3Ł©ÈçÍŒ1ŁŹŚśNGĄÎyÖ᜻OBÓÚGŁŹÈçÍŒŁŹÀûÓĂÒ»ŽÎșŻÊęșͶțŽÎșŻÊęÍŒÏóÉÏ”ă”ÄŚű±êÌŰŐśŁŹÉèNŁšmŁŹ$\frac{1}{2}$m2-$\frac{1}{2}$mŁ©Łš0ŁŒmŁŒ3Ł©ŁŹÔòGŁšmŁŹmŁ©ŁŹÔÙžùŸĘÈęœÇĐÎĂæ»ęč«ÊœŒÆËăłöSĄśAOBŁŹșÍSĄśBONŁŹÈ»șó”Ă”œSËıßĐÎABNOșÍm”ĶțŽÎșŻÊęčŰϔʜŁŹÔÙžùŸĘ¶țŽÎșŻÊę”ÄĐÔÖÊÇóœâŁ»
Łš4Ł©ÉèÖ±ÏßNE”ÄœâÎöÊœÎȘy=px+qŁŹÖ±ÏßENœ»xÖáÓÚHŁŹÖ±ÏßPAœ»OBÓÚQŁŹÈçÍŒ2ŁŹÏÈÀûÓĂŽę¶šÏ”Êę·šÇółöÖ±ÏßNE”ÄœâÎöÊœŁŹÔòżÉÈ·¶šH”ăŚű±êŁŹÔÙրÜRtĄśAOQĄŚRtĄśEOHŁŹÀûÓĂÏàËƱȌÆËăłöOQŁŹÔòÀûÓĂ”ăQÔÚÖ±Ïßy=xÉÏżÉÈ·¶šQ”ăŚű±êŁŹœÓŚĆÀûÓĂŽę¶šÏ”Êę·šÇółöÖ±ÏßAQ”ÄœâÎöÊœŁŹÈ»șóœâÓɶțŽÎșŻÊęÓëÖ±ÏßAQ”ÄœâÎöÊœËùŚéłÉ”Ä·œłÌŚéŒŽżÉ”Ă”œP”ăŚű±êŁź
œâŽđ œâŁșŁš1Ł©ÉèÖ±ÏßAB”ÄœâÎöÊœÎȘy=mx+nŁŹ
°ŃAŁš-1ŁŹ1Ł©ŁŹBŁš3ŁŹ3Ł©ŽúÈë”Ă$\left\{\begin{array}{l}{-m+n=1}\\{3m+n=3}\end{array}\right.$ŁŹœâ”Ă$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=\frac{3}{2}}\end{array}\right.$ŁŹ
ËùÒÔÖ±ÏßAB”ÄœâÎöÊœÎȘy=$\frac{1}{2}$x+$\frac{3}{2}$ŁŹ
”±x=0ʱŁŹy=$\frac{1}{2}$x+$\frac{3}{2}$=$\frac{3}{2}$ŁŹ
ËùÒÔE”ăŚű±êÎȘŁš0ŁŹ$\frac{3}{2}$Ł©Ł»
Łš2Ł©ÉèĆŚÎïÏßœâÎöÊœÎȘy=ax2+bx+cŁŹ
°ŃAŁš-1ŁŹ1Ł©ŁŹBŁš3ŁŹ3Ł©ŁŹOŁš0ŁŹ0Ł©ŽúÈë”Ă$\left\{\begin{array}{l}{a-b+c=1}\\{9a+3b+c=3}\\{c=0}\end{array}\right.$ŁŹœâ”Ă$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$ŁŹ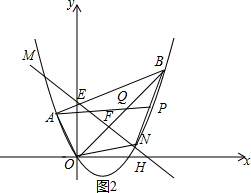
ËùÒÔĆŚÎïÏßœâÎöÊœÎȘy=$\frac{1}{2}$x2-$\frac{1}{2}$xŁ»
Łš3Ł©ÈçÍŒ1ŁŹŚśNGĄÎyÖ᜻OBÓÚGŁŹÈçÍŒŁŹÖ±ÏßOB”ÄœâÎöÊœÎȘy=xŁŹ
ÉèNŁšmŁŹ$\frac{1}{2}$m2-$\frac{1}{2}$mŁ©Łš0ŁŒmŁŒ3Ł©ŁŹÔòGŁšmŁŹmŁ©ŁŹGN=m-Łš$\frac{1}{2}$m2-$\frac{1}{2}$mŁ©=-$\frac{1}{2}$m2+$\frac{3}{2}$mŁŹ
SĄśAOB=SĄśAOE+SĄśBOE=$\frac{1}{2}$ĄÁ1ĄÁ$\frac{3}{2}$+$\frac{1}{2}$ĄÁ$\frac{3}{2}$ĄÁ3=3ŁŹSĄśBON=SĄśONG+SĄśBNG=$\frac{1}{2}$•3•Łš-$\frac{1}{2}$m2+$\frac{3}{2}$mŁ©=-$\frac{3}{2}$m2+$\frac{9}{4}$ŁŹ
ËùÒÔSËıßĐÎABNO=SĄśBON+SĄśAOB=-$\frac{3}{2}$m2+$\frac{9}{4}$+3=-$\frac{3}{4}$Łšm-$\frac{3}{2}$Ł©2+$\frac{75}{16}$
”±m=$\frac{3}{2}$ʱŁŹËıßĐÎABNOĂæ»ę”ÄŚîŽóÖ”ŁŹŚîŽóÖ”ÎȘ$\frac{75}{16}$ŁŹŽËʱN”ăŚű±êÎȘŁš$\frac{3}{2}$ŁŹ$\frac{3}{8}$Ł©Ł»
Łš4Ł©ÉèÖ±ÏßNE”ÄœâÎöÊœÎȘy=px+qŁŹÖ±ÏßENœ»xÖáÓÚHŁŹÖ±ÏßPAœ»OBÓÚQŁŹÈçÍŒ2ŁŹ
°ŃEŁš0ŁŹ$\frac{3}{2}$Ł©ŁŹNŁš$\frac{3}{2}$ŁŹ$\frac{3}{8}$Ł©ŽúÈë”Ă$\left\{\begin{array}{l}{q=\frac{3}{2}}\\{\frac{3}{2}p+q=\frac{3}{8}}\end{array}\right.$ŁŹœâ”Ă$\left\{\begin{array}{l}{p=-\frac{3}{4}}\\{q=\frac{3}{2}}\end{array}\right.$ŁŹ
ËùÒÔÖ±ÏßNE”ÄœâÎöÊœÎȘy=-$\frac{3}{4}$x+$\frac{3}{2}$ŁŹ
”±y=0ʱŁŹ-$\frac{3}{4}$x+$\frac{3}{2}$=0ŁŹœâ”Ăx=2ŁŹÔòHŁš2ŁŹ0Ł©ŁŹ
ĄßAŁš-1ŁŹ1Ł©ŁŹBŁš3ŁŹ3Ł©ŁŹ
ĄàĄÏAOE=45ĄăŁŹĄÏBOE=45ĄăŁŹ
ĄàĄÏAOB=90ĄăŁŹ
ĄßĄÏPAO=ĄÏNEOŁŹ
ĄàRtĄśAOQĄŚRtĄśEOHŁŹ
ĄàOAŁșOE=OQŁșOHŁŹŒŽ$\sqrt{2}$Łș$\frac{3}{2}$=OQŁș2ŁŹœâ”ĂOQ=$\frac{4\sqrt{2}}{3}$ŁŹ
ĄàQŁš$\frac{4}{3}$ŁŹ$\frac{4}{3}$Ł©ŁŹ
ĄàÖ±ÏßAQ”ÄœâÎöÊœÎȘy=$\frac{1}{7}$x+$\frac{8}{7}$ŁŹ
œâ·œłÌŚé$\left\{\begin{array}{l}{y=\frac{1}{7}x+\frac{8}{7}}\\{y=\frac{1}{2}{x}^{2}-\frac{1}{2}x}\end{array}\right.$”Ă$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$»ò$\left\{\begin{array}{l}{x=\frac{16}{7}}\\{y=\frac{72}{49}}\end{array}\right.$ŁŹ
ĄàP”ăŚű±êÎȘŁš$\frac{16}{7}$ŁŹ$\frac{72}{49}$Ł©Łź
”ăÆÀ ±ŸÌâżŒČéÁ˶țŽÎșŻÊę”ÄŚÛșÏÌâŁșÊìÁ·ŐÆÎŐ¶țŽÎșŻÊęÍŒÏóÉÏ”ă”ÄŚű±êÌŰŐśșͶțŽÎșŻÊę”ÄĐÔÖÊŁ»»áÀûÓĂŽę¶šÏ”Êę·šÇó¶țŽÎșŻÊęșÍÒ»ŽÎșŻÊę”ÄĐÔÖÊŁ»ÀíœâŚű±êÓëÍŒĐÎĐÔÖÊŁŹÀûÓĂĂæ»ę”ÄșÍČîŒÆËăČ»čæÔòÍŒĐΔÄĂæ»ęŁź



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
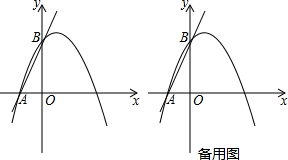
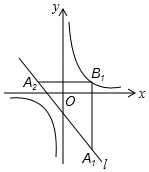 ÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹÒŃÖȘÖ±ÏßlŁșy=-x-1ŁŹË«ÇúÏßy=$\frac{1}{x}$ŁźÔÚÖ±ÏßlÉÏÈĄ”ăA1ŁŹčę”ăA1ŚśxÖá”ÄŽčÏßœ»Ë«ÇúÏßÓÚ”ăB1ŁŹčę”ăB1ŚśyÖá”ÄŽčÏßœ»Ö±ÏßlÓÚ”ăA2ŁŹŒÌĐűČÙŚśŁșčę”ăA2ŚśxÖá”ÄŽčÏßœ»Ë«ÇúÏßÓÚ”ăB2ŁŹčę”ăB2ŚśyÖá”ÄŽčÏßœ»Ö±ÏßlÓÚ”ăA3ŁŹĄŁŹÒÀŽÎŐâŃù”Ă”œË«ÇúÏßÉϔĔăB1ŁŹB2ŁŹB3ŁŹB4ŁŹĄŁŹBnŁźŒÇ”ăA1”ÄșáŚű±êÎȘ2ŁŹÔòB2016”ÄŚű±êÎȘŁš-$\frac{1}{3}$ŁŹ-3Ł©Łź
ÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹÒŃÖȘÖ±ÏßlŁșy=-x-1ŁŹË«ÇúÏßy=$\frac{1}{x}$ŁźÔÚÖ±ÏßlÉÏÈĄ”ăA1ŁŹčę”ăA1ŚśxÖá”ÄŽčÏßœ»Ë«ÇúÏßÓÚ”ăB1ŁŹčę”ăB1ŚśyÖá”ÄŽčÏßœ»Ö±ÏßlÓÚ”ăA2ŁŹŒÌĐűČÙŚśŁșčę”ăA2ŚśxÖá”ÄŽčÏßœ»Ë«ÇúÏßÓÚ”ăB2ŁŹčę”ăB2ŚśyÖá”ÄŽčÏßœ»Ö±ÏßlÓÚ”ăA3ŁŹĄŁŹÒÀŽÎŐâŃù”Ă”œË«ÇúÏßÉϔĔăB1ŁŹB2ŁŹB3ŁŹB4ŁŹĄŁŹBnŁźŒÇ”ăA1”ÄșáŚű±êÎȘ2ŁŹÔòB2016”ÄŚű±êÎȘŁš-$\frac{1}{3}$ŁŹ-3Ł©ŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
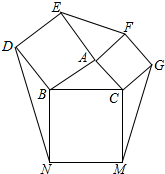 ÈçÍŒŁŹÒÔĄśABC”ıßABĄąACĄąBCÎȘÒ»±ßŁŹ·Ö±đÏòÈęœÇĐΔÄÍâČàŚśŐę·œĐÎABDEŁŹŐę·œĐÎACGFĄąŐę·œĐÎBCMN
ÈçÍŒŁŹÒÔĄśABC”ıßABĄąACĄąBCÎȘÒ»±ßŁŹ·Ö±đÏòÈęœÇĐΔÄÍâČàŚśŐę·œĐÎABDEŁŹŐę·œĐÎACGFĄąŐę·œĐÎBCMNČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
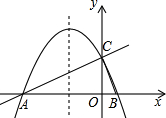 ÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”xOyÖĐŁŹÖ±Ïßy=$\frac{1}{2}$x+2ÓëxÖ᜻ÓÚ”ăAŁŹÓëyÖ᜻ÓÚ”ăCŁŹĆŚÎïÏßy=ax2+bx+c”ĶԳÆÖáÊÇx=-$\frac{3}{2}$ÇÒŸčęAŁŹCÁœ”㣏ÓëxÖá”ÄÁíÒ»œ»”ăÎȘ”ăBŁź
ÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”xOyÖĐŁŹÖ±Ïßy=$\frac{1}{2}$x+2ÓëxÖ᜻ÓÚ”ăAŁŹÓëyÖ᜻ÓÚ”ăCŁŹĆŚÎïÏßy=ax2+bx+c”ĶԳÆÖáÊÇx=-$\frac{3}{2}$ÇÒŸčęAŁŹCÁœ”㣏ÓëxÖá”ÄÁíÒ»œ»”ăÎȘ”ăBŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
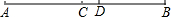 ÈçÍŒŁŹCÊÇÏ߶ÎAB”ÄÖД㣏DÔÚÏ߶ÎCBÉÏŁŹAD=6ŁŹDB=4ŁŹÔòCD”Äł€”ÈÓÚ1Łź
ÈçÍŒŁŹCÊÇÏ߶ÎAB”ÄÖД㣏DÔÚÏ߶ÎCBÉÏŁŹAD=6ŁŹDB=4ŁŹÔòCD”Äł€”ÈÓÚ1ŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | Łš1ŁŹ-4Ł© | BŁź | Łš-1ŁŹ4Ł© | CŁź | Łš-1ŁŹ-4Ł© | DŁź | Łš1ŁŹ4Ł© |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | 4 | BŁź | -4 | CŁź | 6 | DŁź | -6 |
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com