
分析 (1)分OC、OD在边OA的同侧和异侧分别作出图形;
(2)利用余角或补角的性质,根据以上四种情况分别进行计算即可得解.
解答 解:(1)如图所示: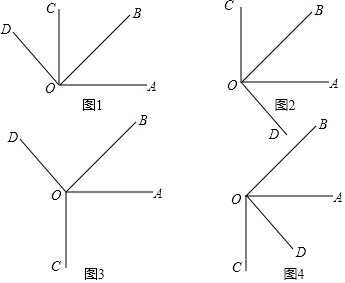
(2)如图1,∵OC⊥OA,OD⊥OB,
∴∠AOB+∠BOC=90°,∠COD+∠BOC=90°,
∴∠COD=∠AOB=30°;
如图2,∵OC⊥OA,OD⊥OB,
∴∠AOC=∠BOD=90°,
∠BOC=∠AOC-∠AOB=90°-30°=60°,
∴∠COD=∠BOD+∠BOC=90°+60°=150°;
如图3,∠COD=360°-∠AOC-∠AOB-∠BOD,
=360°-90°-30°-90°,
=150°;
如图4,∵OC⊥OA,OD⊥OB,
∴∠AOB+∠AOD=90°,∠COD+∠AOD=90°,
∴∠COD=∠AOB=30°.
综上所述,∠COD的度数为30°或150°.
点评 本题考查了垂线的定义,角的计算,同角的余角相等的性质,解题的关键在于分情况讨论、求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
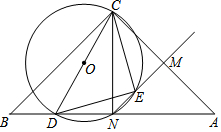 已知△ABC中,∠BCA=90°,BC=AC,D是BA边上一点(点D不与A,B重合),M是CA中点,当以CD为直径的⊙O与BA边交于点N,⊙O与射线NM交于点E,连接CE,DE.
已知△ABC中,∠BCA=90°,BC=AC,D是BA边上一点(点D不与A,B重合),M是CA中点,当以CD为直径的⊙O与BA边交于点N,⊙O与射线NM交于点E,连接CE,DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
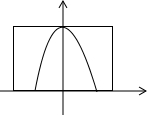 如图,小明家天花板上有个离地面3米高的消防喷淋系统.一天他想试试家里的消防喷淋系统是否管用,第一次他尝试了一下,结果喷洒到地面足够覆盖的范围大约是直径为3米的圆.第二次小明不想弄湿地板于是就找了一个盆口直径为0.6米的脸盆来接水.请问他得把脸盆盆口至少举到多高的位置才可以不让水洒出来?(水从喷水口洒出落地的曲线符合抛物线的路线)( )
如图,小明家天花板上有个离地面3米高的消防喷淋系统.一天他想试试家里的消防喷淋系统是否管用,第一次他尝试了一下,结果喷洒到地面足够覆盖的范围大约是直径为3米的圆.第二次小明不想弄湿地板于是就找了一个盆口直径为0.6米的脸盆来接水.请问他得把脸盆盆口至少举到多高的位置才可以不让水洒出来?(水从喷水口洒出落地的曲线符合抛物线的路线)( )| A. | 2.52米 | B. | 2.88米 | C. | 2.97米 | D. | 3.12米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com