
| A. | 1个 | B. | 2个 | C. | 4个 | D. | 8个 |
分析 设方程的两整数根为α、β,则α2+β2=2009,根据“若两个整数的和为奇数,则两个整数一奇一偶”可得α、β一奇一偶,不妨设假设α=2m,β=2n+1,代入α2+β2=2009,整理得m2+n(n+1)=502,由n(n+1)是偶数可得m也是偶数,可设m=2p,则有2p2+$\frac{1}{2}$n(n+1)=251,可得$\frac{1}{2}$n(n+1)是奇数,只需分n=4q+2和n=4q+1进行讨论,即可得到α、β的值,问题得以解决.
解答 解:设方程的两整数根为α、β,则α2+β2=2009,
由2009是奇数可得α、β一奇一偶,
不妨设假设α=2m,β=2n+1(其中m,n为整数),
则有m2+n2+n=502,即m2+n(n+1)=502,
由n(n+1)是偶数可得m是偶数,
可设m=2p,代入得:2p2+$\frac{1}{2}$n(n+1)=251,
则$\frac{1}{2}$n(n+1)必是奇数,
可设n=4q+2或n=4q+1(其中q为整数),
①当α,β均为正整数时,p、q均为非负整数,
若n=4q+2,则有p2+4q2+5q=124,q取任意非负整数时,p都不是整数;
若n=4q+1时,则有p2+4q2+3q=125,仅当q=4时,p=7,
此时α=2m=4p=28,β=2n+1=2(4q+1)+1=35.
同理:②α,β均为负整数时,α=-28,β=-35;
③当α为正整数,β为负整数时,α=28,β=-35;
④当α为负整数,β为正整数时,α=-28,β=35.
故选C.
点评 本题主要了考查了奇数与偶数、带余除法等知识,在解决问题的过程中用到了“若两个整数的和为奇数,则两个整数一奇一偶”,“两个连续的整数的积为偶数”等重要的结论,另外,还用到了分类讨论的数学思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
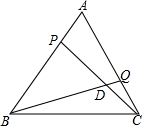 如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点A、C同时出发,运动速度均为1cm/s,点P从点A出发,沿A→B运动,到点B停止,点Q从点C出发,沿C→A运动,到点A停止,连接BQ、CP相交于点D,设点P的运动时间为x(s).
如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点A、C同时出发,运动速度均为1cm/s,点P从点A出发,沿A→B运动,到点B停止,点Q从点C出发,沿C→A运动,到点A停止,连接BQ、CP相交于点D,设点P的运动时间为x(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
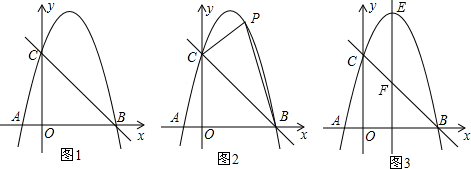
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
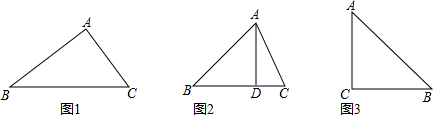
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com