
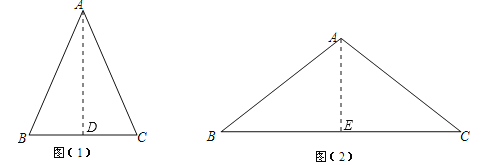
����Ŀ�����Ƕ��壺�����������еױ������ıȽ����ǵ��ڶ�(can)����ͼ�٣�����ABC�У�AB��AC���ǡ�B���ڶԼ���canB����ʱcanB��![]() .����֪��һ���ǵĴ�С������ǵ��ڶ�ֵ��һһ��Ӧ�ģ����������ǵ��ڶԵĶ��壬���������⣺
.����֪��һ���ǵĴ�С������ǵ��ڶ�ֵ��һһ��Ӧ�ģ����������ǵ��ڶԵĶ��壬���������⣺
(1) . can30����______ __��
(2) . ��ͼ�ڣ���֪����ABC�У�AB��AC��canB��![]() ��S��ABC��24������ABC���ܳ���
��S��ABC��24������ABC���ܳ���

���𰸡���1��![]() ����2��18
����2��18![]()
�������������������1������A��AD��BC�ڵ�D��������B=30�����ɵó�BD=![]() AB����ϵ��������ε����ʿɵó�BC=
AB����ϵ��������ε����ʿɵó�BC=![]() AB���̶��ó�canB��
AB���̶��ó�canB��
��2������A��AE��BC�ڵ�E������canB=![]() ����BC=8x��AB=5x������S��ABC=24���ɵó�x��ֵ���̶�����ܳ���
����BC=8x��AB=5x������S��ABC=24���ɵó�x��ֵ���̶�����ܳ���
����������⣺��1������A��AD��BC�ڵ�D���ߡ�B=30������cos��B=![]() =
=![]() ����BD=
����BD=![]() AB���ߡ�ABC�ǵ��������Σ���BC=2BD=
AB���ߡ�ABC�ǵ��������Σ���BC=2BD=![]() AB����can30��=
AB����can30��=![]() =
=![]() ��
��
��2������A��AE��BC�ڵ�E����canB=![]() �������BC=8x��AB=5x����AE=
�������BC=8x��AB=5x����AE=![]() =3x����S��ABC=24����
=3x����S��ABC=24����![]() BC��AE=12x2=24����ã�x=
BC��AE=12x2=24����ã�x=![]() ����AB=AC=
����AB=AC=![]() ��BC=
��BC=![]() ���Ӷ��ɵ���ABC���ܳ�Ϊ
���Ӷ��ɵ���ABC���ܳ�Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
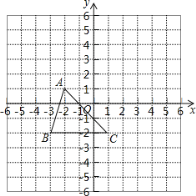
����Ŀ����ͼ����֪��MON=90��A�ǡ�MON�ڲ���һ�㣬����A��AB��ON������Ϊ��B��AB=3���ף�OB=4���ף�����E��Fͬʱ��O���������E��1.5����/����ٶ���ON�����˶�����F��2����/����ٶ���OM�����˶���EF��OA���ڵ�C������AE������E�����Bʱ����F��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1����t=1��ʱ����EOF�릤ABO�Ƿ����ƣ���˵�����ɡ�
��2�����˶������У�����tȡ��ֵʱ������EF��OA��Ϊʲô��
��3������AF�����˶������У��Ƿ����ijһʱ��t��ʹ��S��AEF=![]() S�ı���ABOF �������ڣ��������ʱt��ֵ���������ڣ���˵�����ɡ�
S�ı���ABOF �������ڣ��������ʱt��ֵ���������ڣ���˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
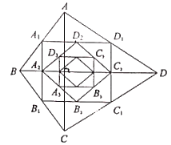
����Ŀ����ͼ��ʾ��������![]() ����
����![]() �ڷ����У�����ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��Ƚ�
�ڷ����У�����ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��Ƚ�![]() ����ƽ��3����λ���ȣ�������ƽ��2����λ���ȣ��õ�
����ƽ��3����λ���ȣ�������ƽ��2����λ���ȣ��õ�![]() ��
��
![]() �������������ֱ��ǣ�
�������������ֱ��ǣ�![]() ______
______![]() ��
��![]() ______
______![]() ��
��![]() ______
______![]() ��
��
![]() ��ͼ�л���
��ͼ�л���![]() ��
��
![]() ƽ�ƺ�
ƽ�ƺ�![]() ��������������ֱ�Ϊ��
��������������ֱ�Ϊ��![]() ______
______![]() ��
��![]() ______
______![]() ��
��![]() ______
______![]() ��
��
![]() ��y����һ��P��ʹ
��y����һ��P��ʹ![]() ��
��![]() �����ȣ���P�������Ϊ______��
�����ȣ���P�������Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ħ�г��ֱ��ij��������6000��A��B����ͬʱ������������У�������ʻһ��ʱ�����C�صļ���Ħ�г����˹��ϣ�����ͣ�µ绰֪ͨ�ң��ҽӵ��绰�������Գ���ʱ�ٶȵ�![]() ����C���������У�����C�غ���5�������˼�Ħ�г���Ȼ�������Գ���ʱ�ٶȵ�
����C���������У�����C�غ���5�������˼�Ħ�г���Ȼ�������Գ���ʱ�ٶȵ�![]() ���������յ�A�����У�������ԭ���ٶ���B���������У�2���Ӻ����ҵ�һ��ά�����������Լ����ϣ�����������ͷ����ԭ�ٶ�
���������յ�A�����У�������ԭ���ٶ���B���������У�2���Ӻ����ҵ�һ��ά�����������Լ����ϣ�����������ͷ����ԭ�ٶ�![]() �����ٶ����ٷ��أ���ʱ��δ����A�أ�.����������У���������·��y���ף���׳�����ʱ��x���֣�֮��Ĺ�ϵ��ͼ��ʾ�������Ҵӵ绰����ͷʱ����Բ��ƣ����ҵ���A��ʱ������A�صľ���Ϊ ________��.
�����ٶ����ٷ��أ���ʱ��δ����A�أ�.����������У���������·��y���ף���׳�����ʱ��x���֣�֮��Ĺ�ϵ��ͼ��ʾ�������Ҵӵ绰����ͷʱ����Բ��ƣ����ҵ���A��ʱ������A�صľ���Ϊ ________��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �У�
�У�![]() ˳�������ı���
˳�������ı���![]() �����е㣬�õ��ı���
�����е㣬�õ��ı���![]() ����˳�������ı���
����˳�������ı���![]() �����е㣬�õ��ı���
�����е㣬�õ��ı���![]() ...��˽�����ȥ���õ��ı���
...��˽�����ȥ���õ��ı���![]() �����н�����ȷ�ĸ����У� ��
�����н�����ȷ�ĸ����У� ��
���ı���![]() �Ǿ��Σ����ı���
�Ǿ��Σ����ı���![]() �����Σ����ı���
�����Σ����ı���![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() �� ���ı���
�� ���ı���![]() �������
�������![]() ��
��
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90������B=30������AΪԲ�ģ����ⳤΪ�뾶�����ֱ�AB��AC�ڵ�M��N���ٷֱ���M��NΪԲ�ģ�����![]() MN�ij�Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�D. ���н��ۣ���AD�ǡ�BAC��ƽ���ߣ��ڵ�D��AB�Ĵ�ֱƽ�����ϣ��ۡ�ADC=60�㣻��
MN�ij�Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�D. ���н��ۣ���AD�ǡ�BAC��ƽ���ߣ��ڵ�D��AB�Ĵ�ֱƽ�����ϣ��ۡ�ADC=60�㣻��![]() ��������ȷ�Ľ����У� ��
��������ȷ�Ľ����У� ��
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
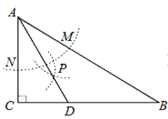
����Ŀ����֪����ͼ������ƽ���ı���ABCD�У�AB=3cm��BC=5cm��AC��AB����ACD��AC�ķ�������ƽ�Ƶõ���PNM���ٶ�Ϊ1cm/s��ͬʱ����Q�ӵ�C����������CB���������ƶ����ٶ�Ϊ1cm/s������PNMֹͣƽ��ʱ����QҲֹͣ�ƶ�����ͼ�������ƶ�ʱ��Ϊt��s����0��t��4��������PQ��MQ��MC������������⣺

��1����tΪ��ֵʱ��PQ��AB��
��2����t=3ʱ������QMC�������
��3���Ƿ����ijһʱ��t��ʹPQ��MQ�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ACB�͡�ECD���ǵ���ֱ�������Σ���ACB����ECD��90�㣬DΪAB����һ�㣮
(1)��֤����ACE�ա�BCD��
(2)��AD��5��BD��12����DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0���Ĵ���ͼ����ͼ�����ڸö��κ���������˵��������ǣ� ��

A. ��������Сֵ
B. �Գ�����ֱ��x=![]()
C. ��x��![]() ��y��x���������С
��y��x���������С
D. ����1��x��2ʱ��y��0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com