
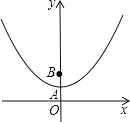
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+![]() 与y轴相交于点A,点B与点O关于点A对称
与y轴相交于点A,点B与点O关于点A对称
(1)填空:点B的坐标是 ;
(2)过点B的直线y=kx+b(其中k<0)与x轴相交于点C,过点C作直线l平行于y轴,P是直线l上一点,且PB=PC,求线段PB的长(用含k的式子表示),并判断点P是否在抛物线上,说明理由;
(3)在(2)的条件下,若点C关于直线BP的对称点C′恰好落在该抛物线的对称轴上,求此时点P的坐标.
【答案】(1)(0,![]() );(2)点P在抛物线上,理由详见解析;(3)P点坐标为(
);(2)点P在抛物线上,理由详见解析;(3)P点坐标为(![]() ,1).
,1).
【解析】
试题分析:(1)由抛物线解析式可求得点A的坐标,再利用对称可求得B点坐标;(2)可先用k表示出C点坐标,过B作BD⊥l于点D,条件可知P点在x轴上方,设P点纵坐标为y,可表示出PD、PB的长,在Rt△PBD中,利用勾股定理可求得y,则可求出PB的长,此时可得出P点坐标,代入抛物线解析式可判断P点在抛物线上;(3)利用平行线和轴对称的性质可得到∠OBC=∠CBP=∠C′BP=60°,则可求得OC的长,代入抛物线解析式可求得P点坐标.
试题解析:(1)∵抛物线y=x2+![]() 与y轴相交于点A,
与y轴相交于点A,
∴A(0,![]() ),
),
∵点B与点O关于点A对称,
∴BA=OA=![]() ,
,
∴OB=![]() ,即B点坐标为(0,
,即B点坐标为(0,![]() ),
),
故答案为:(0,![]() );
);
(2)∵B点坐标为(0,![]() ),
),
∴直线解析式为y=kx+![]() ,令y=0可得kx+
,令y=0可得kx+![]() =0,解得x=﹣
=0,解得x=﹣![]() ,
,
∴OC=﹣![]() ,
,
∵PB=PC,
∴点P只能在x轴上方,
如图1,过B作BD⊥l于点D,设PB=PC=m,
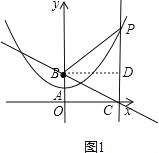
则BD=OC=﹣![]() ,CD=OB=
,CD=OB=![]() ,
,
∴PD=PC﹣CD=m﹣![]() ,
,
在Rt△PBD中,由勾股定理可得PB2=PD2+BD2,
即m2=(m﹣![]() )2+(﹣
)2+(﹣![]() )2,解得m=
)2,解得m=![]() +
+![]() ,
,
∴PB=![]() +
+![]() ,
,
∴P点坐标为(﹣![]() ,
,![]() +
+![]() ),
),
当x=﹣![]() 时,代入抛物线解析式可得y=
时,代入抛物线解析式可得y=![]() +
+![]() ,
,
∴点P在抛物线上;
(3)如图2,连接CC′,
∵l∥y轴,
∴∠OBC=∠PCB,
又PB=PC,
∴∠PCB=∠PBC,
∴∠PBC=∠OBC,
又C、C′关于BP对称,且C′在抛物线的对称轴上,即在y轴上,
∴∠PBC=∠PBC′,
∴∠OBC=∠CBP=∠C′BP=60°,
在Rt△OBC中,OB=![]() ,则BC=1
,则BC=1
∴OC=![]() ,即P点的横坐标为
,即P点的横坐标为![]() ,代入抛物线解析式可得y=(
,代入抛物线解析式可得y=(![]() )2+
)2+![]() =1,
=1,
∴P点坐标为(![]() ,1).
,1).


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】李老师给同学们布置了以下解方程的作业,作业要求是无实数根的方程不用解,不用解的方程是( )
A.x2﹣x=0B.x2+x=0C.x2+x﹣1=0D.x2+1=0
查看答案和解析>>
科目:初中数学 来源: 题型:
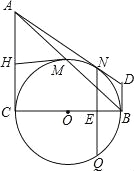
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH.
(1)求证:MH为⊙O的切线.
(2)若MH=![]() ,tan∠ABC=
,tan∠ABC=![]() ,求⊙O的半径.
,求⊙O的半径.
(3)在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于N点,过N点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段NQ的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校开展的“爱我中华”的一次演讲比赛中,编号1,2,3,4,5,6的五位同学最后成绩如表所示.那么这五位同学演讲成绩的众数与中位数依次是( )
参赛者编号 | 1 | 2 | 3 | 4 | 5 | 6 |
成绩/分 | 95 | 88 | 90 | 93 | 88 | 92 |
A. 92,88 B. 88,90 C. 88,92 D. 88,91
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A.对角线互相垂直的四边形是菱形B.对角形相等的四边形是矩形
C.顺次连结平行四边形各边中点所得四边形是平行四边形D.一组邻边相等的平行四边形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com