
【题目】等腰三角形的一个角是70°,则它的一个底角的度数是( )
A. 70° B. 70°或55° C. 80° D. 55°
科目:初中数学 来源: 题型:
【题目】△ABC中,①若AB=BC=CA,则△ABC是等边三角形;②属于轴对称图形,且有一个角为60°的三角形是等边三角形;③有三条对称轴的三角形是等边三角形;④有两个角是60°的三角形是等边三角形,上述结论中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
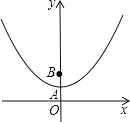
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+![]() 与y轴相交于点A,点B与点O关于点A对称
与y轴相交于点A,点B与点O关于点A对称
(1)填空:点B的坐标是 ;
(2)过点B的直线y=kx+b(其中k<0)与x轴相交于点C,过点C作直线l平行于y轴,P是直线l上一点,且PB=PC,求线段PB的长(用含k的式子表示),并判断点P是否在抛物线上,说明理由;
(3)在(2)的条件下,若点C关于直线BP的对称点C′恰好落在该抛物线的对称轴上,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
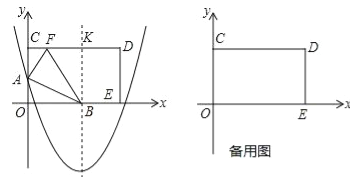
【题目】如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y=![]() x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
①点B的坐标为( 、 ),BK的长是 ,CK的长是 ;
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com