
【题目】在正方形ABCD中,点H,E,F分别在边AB,BC,CD上,AE⊥HF于点G.
(1)如图1,求证:AE=HF;
(2)如图2,延长FH,交CB的延长线于M,连接AC,交HF于N.若MB=BE,EC=2BE,求![]() 的值;
的值;
(3)如图3,若AB=2,BH=DF,将线段HF绕点F顺时针旋转90°至线段MF,连接AM,则线段AM的最小值为 .(直接写出结果)
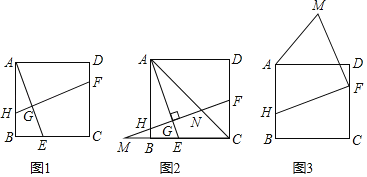
【答案】(1)见解析;(2)![]() =2;(3)AM的最小值为
=2;(3)AM的最小值为![]() .
.
【解析】
(1)如图1中,作HM⊥CD于M.证明△ABE≌△HMF(ASA),即可推出AE=HF.
(2)不妨设BE=BM=a,EC=2a,则AB=BC=CD=3a,CM=4a,推出tan∠BAE=![]() =
=![]() ,证明∠M=∠BAE,推出tan
,证明∠M=∠BAE,推出tan![]() =
=![]() ,可得BH=
,可得BH=![]() a,CF=
a,CF=![]() a,推出AH=AB﹣BH=3a﹣
a,推出AH=AB﹣BH=3a﹣![]() a=
a=![]() a,再利用相似三角形的性质即可解决问题.
a,再利用相似三角形的性质即可解决问题.
(3)如图3中,延长BA到N,使得AN=AD,作MJ⊥AN于J,交CD的延长线于K,作FQ⊥AB于Q,则四边形BCFQ,四边形ADKJ都是矩形,△FQH≌△FKM(AAS).想办法证明tan∠N=2,推出点M的运动轨迹是射线NM,∠N是的定值,作AP⊥MN于P,根据垂线段最短可知:当AM与AP重合时,AM的值最小.
(1)证明:如图1中,作HM⊥CD于M.
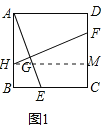
∴四边形ABC都是正方形,
∴∠B=∠C=∠CMH=90°,AB=BC,
∴四边形BCMH是矩形,
∴HM=BC=AB,
∵AE⊥HF,
∴∠AGH=∠AHM=90°,
∴∠BAE+∠AHG=90°,∠AHG+∠FHM=90°,
∴∠BAE=∠FHM,∵∠B=∠HMF=90°,
∴△ABE≌△HMF(ASA),
∴AE=HF.
(2)解:如图2中,
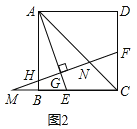
∵EC=2BE,不妨设BE=BM=a,EC=2a,则AB=BC=CD=3a,CM=4a,
∴tan∠BAE=![]() =
=![]() ,
,
∵ABE=∠MGE=90°,
∴∠BAE+∠AEB=90°,∠M+∠AEB=90°,
∴∠M=∠BAE,
∴tan![]() =
=![]()
∴BH=![]() a,CF=
a,CF=![]() a,
a,
∴AH=AB﹣BH=3a﹣![]() a=
a=![]() a,
a,
∴CF∥AH,
∴△ANH∽△CNF,
∴![]() =
=![]() =
=![]() =2.
=2.
(3)解:如图3中,延长BA到N,使得AN=AD,作MJ⊥AN于J,交CD的延长线于K,作FQ⊥AB于Q,则四边形BCFQ,四边形ADKJ都是矩形,
∵∠QFH+∠QFM=∠KFM+∠QFM
∴∠QFH=∠KFM
∵∠FQH =∠FKM =90°,HF=MF
∴△FQH≌△FKM(AAS).

∴QK=KM,DF=AQ=BH,
∵KJ=AD=AB,
∴JM=AQ+BH=2AQ,
∵FK=FQ=JQ=AD=AN,
∴AQ=JN,
∴JM=2JN,
∴tan∠N=![]() =2,
=2,
∴点M的运动轨迹是射线NM,∠N是的定值,作AP⊥MN于P,
根据垂线段最短可知:当AM与AP重合时,AM的值最小,
∵tan∠N=![]() =2,设NP=x,AP=2x,
=2,设NP=x,AP=2x,
在Rt△APN中,则有22=x2+4x2,
解得x=![]() (负根已经舍弃),
(负根已经舍弃),
∴PA=2x=![]() ,
,
∴AM的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,△ABC直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC顺时针旋转后能与△EBD重合,那么:
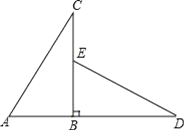
(1)旋转中心是哪一点?旋转角是多少度?
(2)AC与DE的关系怎样?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,交y轴于点E.
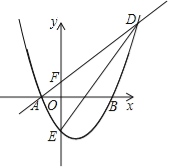
(1)求此抛物线的解析式.
(2)若直线y=x+1与抛物线交于A、D两点,与y轴交于点F,连接DE,求△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 0 | p | m | 3 |
| q | 0 | … |
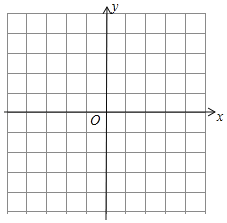
(1)求这个二次函数的表达式;
(2)表格中字母m= ;(直接写出答案)
(3)在给定的直角坐标系中,画出这个二次函数的图象;
(4)以上二次函数的图象与x轴围成的封闭区域内(不包括边界),横、纵坐标都是整数的点共有 个.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
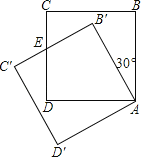
【题目】如图,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C'D',边B'C'交CD于点E.若正方形ABCD的边长为3,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点, AD与过点C的直线互相垂直,垂足为点D,AD交⊙O于点E,AC平分∠DAB,连接CE,CB.
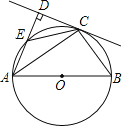
(1)求证:CD是⊙O的切线;
(2)若AC=![]() ,CE=
,CE=![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com