
【题目】如图,在△ABC中,∠A=640,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;∠A2BC和∠A2CD的平分线交于点A3,则∠A5= ______ .

科目:初中数学 来源: 题型:
【题目】如图,点D,E在△ABC的边BC上,连接AD,AE. ①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:(1)①②![]() ③;(2)①③
③;(2)①③![]() ②;(3)②③
②;(3)②③![]() ①.
①.

(1)以上三个命题是真命题的为(直接答题号) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)当a=2,b=![]() 时,分别求代数式a2﹣2ab+b2和(a﹣b)2的值;
时,分别求代数式a2﹣2ab+b2和(a﹣b)2的值;
(2)当a=﹣5,b=﹣3时,a2﹣2ab+b2 (a﹣b)2(填“=“,“<”“>”)
(3)观察(1)(2)中代探索代数式a2﹣2ab+b2和(a﹣b)2有何数量关系,并把探索的结果写出来:a2﹣2ab+b2 (a﹣b)2(填“=”,“<”“>”)
(4)利用你发现的规律,求135.72﹣2×135.7×35.7+35.72的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
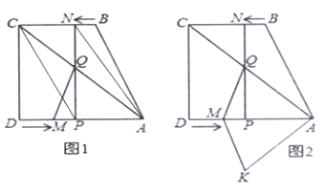
【题目】如图1,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,同时,点
运动,同时,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度向点
出发,以每秒1个单位长度的速度向点![]() 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
(1)连接![]() 、
、![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 为平行四边形;
为平行四边形;
(2)求出点![]() 到
到![]() 的距离;
的距离;
(3)如图2,将![]() 沿
沿![]() 翻折,得
翻折,得![]() ,是否存在某时刻
,是否存在某时刻![]() ,使四边形
,使四边形![]() 为菱形,若存在,求
为菱形,若存在,求![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
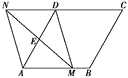
【题目】如图所示,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)①当AM为何值时,四边形AMDN是矩形?
②当AM为何值时,四边形AMDN是菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)判断BE与CF的数量关系,并说明理由;
(2)如果AB=8,AC=6,求AE、BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点D,E为圆心,大于![]() DE的长为半径作弧,两弧交于F;
DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高. 其中顺序正确的作图步骤是( )

A. ①②③④ B. ④③②① C. ②④③① D. ④③①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com