
【题目】如图1,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,同时,点
运动,同时,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度向点
出发,以每秒1个单位长度的速度向点![]() 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
(1)连接![]() 、
、![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 为平行四边形;
为平行四边形;
(2)求出点![]() 到
到![]() 的距离;
的距离;
(3)如图2,将![]() 沿
沿![]() 翻折,得
翻折,得![]() ,是否存在某时刻
,是否存在某时刻![]() ,使四边形
,使四边形![]() 为菱形,若存在,求
为菱形,若存在,求![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
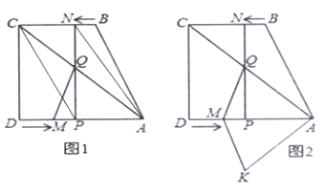
【答案】(1)当![]() 时,四边形
时,四边形![]() 为平行四边形;(2)点
为平行四边形;(2)点![]() 到
到![]() 的距离
的距离![]() ;(3)存在,
;(3)存在,![]() ,使四边形
,使四边形![]() 为菱形.
为菱形.
【解析】
(1)先判断出四边形CNPD为矩形,然后根据四边形![]() 为平行四边形得
为平行四边形得![]() ,即可求出t值;
,即可求出t值;
(2)设点![]() 到
到![]() 的距离
的距离![]() ,利用勾股定理先求出AC,然后根据
,利用勾股定理先求出AC,然后根据![]() 面积不变求出点
面积不变求出点![]() 到
到![]() 的距离;
的距离;
(3)由NP⊥AD,QP=PK,可得当PM=PA时有四边形AQMK为菱形,列出方程6-t-2t=8-(6-t),求解即可.
解:(1)根据题意可得,![]()
∵在四边形ABCD中,AD∥BC,∠ADC=90°,NP⊥AD于点P,
∴四边形CNPD为矩形,
∴![]()
∴![]()
∵四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,
∴![]()
解得:![]() ,
,
∴当![]() 时,四边形
时,四边形![]() 为平行四边形;
为平行四边形;
(2)设点![]() 到
到![]() 的距离
的距离![]() ,
,
在![]() 中,
中,
![]() ,
,
在![]() 中,
中,
![]()
![]()
∴![]()
∴点![]() 到
到![]() 的距离
的距离![]()
(3)存在. 理由如下:
∵将![]() 沿
沿![]() 翻折得
翻折得![]()
∵![]() ,
,
∴当![]() 时有四边形
时有四边形![]() 为菱形,
为菱形,
∴![]() ,
,
解得![]() ,
,
∴![]() ,使四边形
,使四边形![]() 为菱形.
为菱形.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数![]() (k≠0)的图象经过圆心P,则k=________________。
(k≠0)的图象经过圆心P,则k=________________。
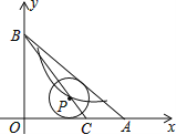
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学积极倡导阳光体育运动,提高中学生身体素质,开展跳绳比赛,下表为该校6年1班40人参加跳绳比赛的情况,若标准数量为每人每分钟100个.

(1)求6年1班40人一分钟内平均每人跳绳多少个?
(2)规定跳绳超过标准数量,每多跳1个绳加3分;规定跳绳未达到标准数量,每少跳1个绳,扣1分,若班级跳绳总积分超过250分,便可得到学校的奖励,通过计算说明6年1班能否得到学校奖励?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)已知点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交直线
轴的直线,交直线![]() 于点
于点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交函数
轴的直线,交函数![]() 的图象于点
的图象于点![]() .
.
①当![]() 时,判断线段
时,判断线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
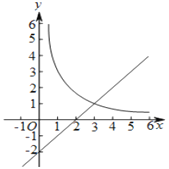
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=640,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;∠A2BC和∠A2CD的平分线交于点A3,则∠A5= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.

(1)如图1,当点E、F在线段AD上时,求证:∠DAG=∠DCG;
(2)如图1,猜想AG与BE的位置关系,并加以证明;
(3)如图2,在(2)条件下,连接HO,试说明HO平分∠BHG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,以
,以![]() 为边在数轴的上方作正方形ABCD.动点
为边在数轴的上方作正方形ABCD.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴正方向匀速运动,同时动点
个单位长度的速度沿数轴正方向匀速运动,同时动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 匀速运动,到达
匀速运动,到达![]() 点后再以同样的速度沿数轴正方向匀速运动,设运动时间为
点后再以同样的速度沿数轴正方向匀速运动,设运动时间为![]() 秒
秒![]() .
.
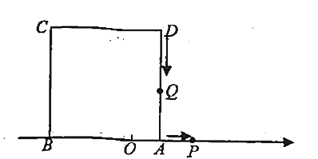
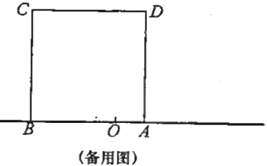
(1)若点![]() 在线段
在线段![]() .上运动,当t为何值时,
.上运动,当t为何值时,![]() ?
?
(2)若点![]() 在线段
在线段![]() 上运动,连接
上运动,连接![]() ,当t为何值时,三角形
,当t为何值时,三角形![]() 的面积等于正方形
的面积等于正方形![]() 面积的
面积的![]() ?
?
(3)在点![]() 和点
和点![]() 运动的过程中,当
运动的过程中,当![]() 为何值时,点
为何值时,点![]() 与点
与点![]() 恰好重合?
恰好重合?
(4)当点![]() 在数轴上运动时,是否存在某-时刻t,使得线段
在数轴上运动时,是否存在某-时刻t,使得线段![]() 的长为
的长为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com