
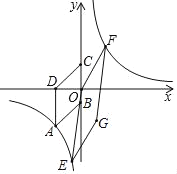
【题目】如图,在平面直角坐标系中,四边形ABCD为菱形,且点D(﹣4,0)在x轴上,点B和点C(0,3)在y轴上,反比例函数y=![]() (k≠0)过点A,点E(﹣2,m)、点F分别是反比例函数图象上的点,其中点F在第一象限,连结OE、OF,以线段OE、OF为邻边作平行四边形OEGF.
(k≠0)过点A,点E(﹣2,m)、点F分别是反比例函数图象上的点,其中点F在第一象限,连结OE、OF,以线段OE、OF为邻边作平行四边形OEGF.
(1)写出反比例函数的解析式;
(2)当点A、O、F在同一直线上时,求出点G的坐标;
(3)四边形OEGF周长是否有最小值?若存在,求出这个最值,并确定此时点F的坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)点G的坐标为(2,﹣5);(3)点F的坐标为(2
;(2)点G的坐标为(2,﹣5);(3)点F的坐标为(2![]() ,2
,2![]() )时,四边形OEGF周长最小,最小值为:4
)时,四边形OEGF周长最小,最小值为:4![]() +4
+4![]() .
.
【解析】
(1)首先根据D点坐标,写出A点的横坐标,再计算CD的长,根据菱形的性质,可得A点的坐标,代入反比例函数,即可求得k的值,进而求得反比例函数的解析式.
(2)首先将E点代入反比例函数,计算m,根据反比例函数的对称性,可得F点的坐标,再证明△ENO≌△FMG,故求得G点坐标.
(3)设出F点的坐标,利用勾股定理列方程,利用二次函数求解.
解:(1)∵点D(﹣4,0)在x轴上,
∴A点横坐标为:﹣4,
∵点C(0,3)在y轴上,
∴DC=5,
∵四边形ABCD为菱形,
∴AD=5,
∴点A的坐标为(﹣4,﹣5),
则解析式为:![]() ;
;
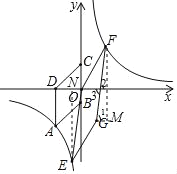
(2)如图,∵x=﹣2时,y=![]() =﹣10,
=﹣10,
∴点E的坐标为(﹣2,﹣10),
∵点A、O、F在同一直线上,
∴A,F关于原点对称,
∴点F的坐标(4,5),
分别过点E、F作EN⊥x轴于点N,FM⊥GM于点M,FM也垂直于x轴,
∵四边形OEGF是平行四边形,
∴EO∥FG,
∴∠NOE=∠3,
∵∠2=∠3=∠1,
∴∠1=∠NOE,
在△ENO和△FMG中
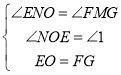 ,
,
∴△ENO≌△FMG(AAS),
设点G的坐标为(m,n),则5﹣n=10,m﹣4=﹣2,
故n=﹣5,m=2,
则点G的坐标为(2,﹣5);
(3)由于OE为定值,则只需求出OF的最小值即可,
设点F的坐标为(a,![]() ),
),
根据勾股定理得,![]() ,
,
显然当a=![]() 时,OF2最小,即a=2
时,OF2最小,即a=2![]() 时,OF最小,OF=2
时,OF最小,OF=2![]() ,
,
EO=2![]() ,
,
因此,当点F的坐标为(2![]() ,2
,2![]() )时,四边形OEGF周长最小,
)时,四边形OEGF周长最小,
最小值为:4![]() +4
+4![]() .
.


科目:初中数学 来源: 题型:
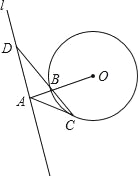
【题目】如图,直线l与⊙O相离,OA⊥l于点A,交⊙O于点B,点C是⊙O上一点,连接CB并延长交直线l于点D,使AC=AD.
(1)求证:AC是⊙O的切线;
(2)若BD=2![]() ,OA=4,求线段BC的长.
,OA=4,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的有( )
①用两颗钉子就可以把木条固定在墙上
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上。
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
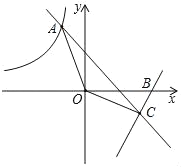
【题目】如图,直线y1=kx+2与反比例函数y2=![]() (x<0)相交于点A,且当x<﹣1时,y1>y2,当﹣1<x<0时,y1<y2.
(x<0)相交于点A,且当x<﹣1时,y1>y2,当﹣1<x<0时,y1<y2.
(1)求出y1的解析式;
(2)若直线y=2x+b与x轴交于点B(3,0),与y1交于点C,求出△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
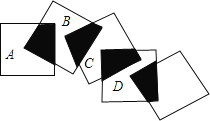
A.2cm2 B.4cm2 C.6cm2 D.8cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是由一些火柴棒搭成的图案:

(1)摆第①个图案用 根火柴棒,摆第②个图案用 根火柴棒,摆第③个图案用 根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案?
查看答案和解析>>
科目:初中数学 来源: 题型:
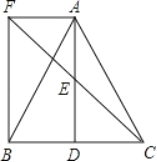
【题目】如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:△AEF≌△DEC;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条公路的转弯处是一段圆弧(![]() ).
).
(1)用直尺和圆规作出![]() 所在圆的圆心
所在圆的圆心![]() ;(要求保留作图痕迹,不写作法)
;(要求保留作图痕迹,不写作法)
(2)若![]() 的中点
的中点![]() 到
到![]() 的距离为
的距离为![]() m,
m,![]() m,求
m,求![]() 所在圆的半径.
所在圆的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com