
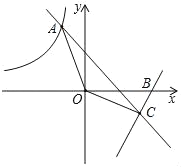
【题目】如图,直线y1=kx+2与反比例函数y2=![]() (x<0)相交于点A,且当x<﹣1时,y1>y2,当﹣1<x<0时,y1<y2.
(x<0)相交于点A,且当x<﹣1时,y1>y2,当﹣1<x<0时,y1<y2.
(1)求出y1的解析式;
(2)若直线y=2x+b与x轴交于点B(3,0),与y1交于点C,求出△AOC的面积.
【答案】(1)y1=﹣x+2;(2)S△AOC=![]() .
.
【解析】
(1)根据当x<﹣1时,y1>y2,当﹣1<x<0时,y1<y2。可得A点的横坐标,再将A点的横坐标代入反比例函数,计算A点的纵坐标,因此可得A点的坐标,代入一次函数,可得k的值,即可的一次函数的解析式.
(2)根据B点的坐标计算b的值,在联立方程组计算C点的坐标,再求出直线y1与x轴的交点,进而计算面积.
解:(1)∵当x<﹣1时,y1>y2,当﹣1<x<0时,y1<y2,
∴点A的横坐标为﹣1,
当x=﹣1时,y=![]() =3,则A(﹣1,3),
=3,则A(﹣1,3),
把A(﹣1,3)代入y=kx+2得﹣k+2=3,解得k=﹣1
∴y1的解析式为y1=﹣x+2;
(2)∵y=2x+b与x轴交于点B(3,0),
∴6+b=0,解得b=﹣6,
∴直线BC的解析式为y=2x﹣6,
解方程组![]() 得
得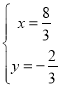 ,则点C的坐标为(
,则点C的坐标为(![]() ,
,![]() ),
),
直线y=﹣x+2与y轴的交点坐标为(2,0),
∴S△AOC=![]() ×(3+
×(3+![]() )×2=
)×2=![]() .
.


科目:初中数学 来源: 题型:
【题目】某检修小组乘一辆汽车沿东西方向方向检修路,约定向东走为正,某天从![]() 地出发到收工时行走记录(单位:
地出发到收工时行走记录(单位:![]() ):
):![]() ,求:
,求:
(1)收工时检修小组在![]() 地的在哪一边,距
地的在哪一边,距![]() 地多远?
地多远?
(2)若汽车耗油![]() 升/每千米,开工时储存
升/每千米,开工时储存![]() 升汽油,用到收工时中途是否需要加油;
升汽油,用到收工时中途是否需要加油;
(3)若加油,最少加多少升才能保证收工后返回![]() 地?若不需要加油,到收工时,还剩多少升汽油?
地?若不需要加油,到收工时,还剩多少升汽油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区实施课堂教学改革后,学生的自主学习、合作交流能力有很大提高,为了解学生自主学习、合作交流的具体情况,张老师对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
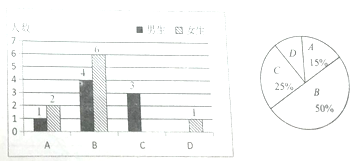
(1)本次调查中,张老师一共调查了_____名同学;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平行四边形ABCD的周长是26cm,对角线AC与BD相交于点O, AC⊥AB,E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE =_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE,OF,OG分别是∠AOC,∠BOD,∠BOC的平分线,以下说法不正确的是( )
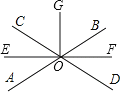
A.∠DOF与∠COG互为余角
B.∠COG与∠AOG互为补角
C.射线OE,OF不一定在同一条直线上
D.射线OE,OG互相垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
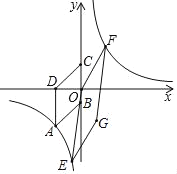
【题目】如图,在平面直角坐标系中,四边形ABCD为菱形,且点D(﹣4,0)在x轴上,点B和点C(0,3)在y轴上,反比例函数y=![]() (k≠0)过点A,点E(﹣2,m)、点F分别是反比例函数图象上的点,其中点F在第一象限,连结OE、OF,以线段OE、OF为邻边作平行四边形OEGF.
(k≠0)过点A,点E(﹣2,m)、点F分别是反比例函数图象上的点,其中点F在第一象限,连结OE、OF,以线段OE、OF为邻边作平行四边形OEGF.
(1)写出反比例函数的解析式;
(2)当点A、O、F在同一直线上时,求出点G的坐标;
(3)四边形OEGF周长是否有最小值?若存在,求出这个最值,并确定此时点F的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③关于x的方程kx﹣x=a﹣b的解是x=3;④当x<3时,y1<y2中.则正确的序号有________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边AC,BC上,
分别在边AC,BC上,![]() ,连接BD,点F,P,G分别为AB,BD,DE的中点.
,连接BD,点F,P,G分别为AB,BD,DE的中点.
(1)如图1中,线段PF与PG的数量关系是 ,位置关系是 ;
(2)若把△ CDE绕点C逆时针方向旋转到图2的位置,连接AD,BE,GF,判断△ FGP的形状,并说明理由;
(3)若把△ CDE绕点C在平面内自由旋转,AC=8,CD=3,请求出△FGP面积的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com