
【题目】某检修小组乘一辆汽车沿东西方向方向检修路,约定向东走为正,某天从![]() 地出发到收工时行走记录(单位:
地出发到收工时行走记录(单位:![]() ):
):![]() ,求:
,求:
(1)收工时检修小组在![]() 地的在哪一边,距
地的在哪一边,距![]() 地多远?
地多远?
(2)若汽车耗油![]() 升/每千米,开工时储存
升/每千米,开工时储存![]() 升汽油,用到收工时中途是否需要加油;
升汽油,用到收工时中途是否需要加油;
(3)若加油,最少加多少升才能保证收工后返回![]() 地?若不需要加油,到收工时,还剩多少升汽油?
地?若不需要加油,到收工时,还剩多少升汽油?
【答案】(1)收工时在A地的正东方向,距A地39km;(2)到收工时中途需要加油;(3)最少加13.2升油才能保证收工后返回![]() 地
地
【解析】
(1)把所有数据相加,根据结果判定方向与距离;
(2)算出走的总路程,得出耗油量,与18比较得出答案即可.
(3)算出从A地出发到收工后返回![]() 地时的耗油量,减去18即可
地时的耗油量,减去18即可
解:(1)(+15)+(-2)+(+5)+(-1)+(+10)+(-3)+(-2)+(+12)+(+4)+(-5)+(+6)=39.
故收工时在A地的正东方向,距A地39km.
(2)从A地出发到收工时汽车共走了:|+15|+|-2|+|+5|+|-1|+|+10|+|-3|+|-2|+|+12|+|+4|+|-5|+|+6|=65km;
∴从A地出发到收工时耗油量为65×0.3=19.5(升).
∵19.5![]() .
.
∴到收工时中途需要加油.
(3)收工后返回![]() 地的耗油量为:39×0.3=11.7(升)
地的耗油量为:39×0.3=11.7(升)
19.5+11.7-18=13.2(升)
∴最少加13.2升才能保证收工后返回![]() 地.
地.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解答下列问题:
题:分解因式:![]()
解:将“![]() ”看成整体,设
”看成整体,设![]() ,则原式=
,则原式=![]()
![]()
再将“![]() ”还原,得原式=
”还原,得原式=![]() .
.
上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你仿照上面的方法解答下列问题:
(1)因式分解:![]() ;
;![]() .
.
(2)因式分解:![]() ;
;![]() .
.
(3)求证:若![]() 为正整数,则式子
为正整数,则式子![]() 的值一定是某一个正整数的平方.
的值一定是某一个正整数的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
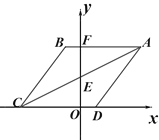
【题目】如图O为坐标原点,四边形ABCD是菱形,A(4,4),B点在第二象限,AB=5,AB与y轴交于点F,对角线AC交y轴于点E
(1)直接写出B、C点的坐标;
(2)动点P从C点出发以每秒1个单位的速度沿折线段C﹣D﹣A运动,设运动时间为t秒,请用含t的代数式表示△EDP的面积;
(3)在(2)的条件下,是否存在一点P,使△APE沿其一边翻折构成的四边形是菱形?若存在,请直接写出当t为多少秒时存在符合条件的点P;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=2,BC=4.点D是线段BC上的一个动点.点D与点B、C不重合,过点D作DE⊥BC交AB于点E,将△ABC沿着直线DE翻折,使点B落在直线BC上的F点.
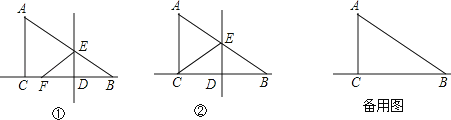
(1)设∠BAC=α(如图①),求∠AEF的大小;(用含α的代数式表示)
(2)当点F与点C重合时(如图②),求线段DE的长度;
(3)设BD=x,△EDF与△ABC重叠部分的面积为S,试求出S与x之间函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 所示,用 20 m 的篱笆(细线部分),两面靠墙围成矩形的苗圃.
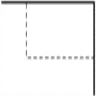
(1)设矩形的一边长为x(m),面积为y(m 2 ),求y关于x的函数表达式;
(2)求当x取8、9、10、11、12时y的值,并观察这几种情况下,哪种情况面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
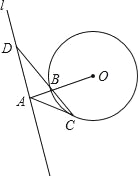
【题目】如图,直线l与⊙O相离,OA⊥l于点A,交⊙O于点B,点C是⊙O上一点,连接CB并延长交直线l于点D,使AC=AD.
(1)求证:AC是⊙O的切线;
(2)若BD=2![]() ,OA=4,求线段BC的长.
,OA=4,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.
(1)求证:△ABD∽△CBA;
(2)在原图上作DE∥AB交AC与点E,请直接写出另一个与△ABD相似的三角形,并求出DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
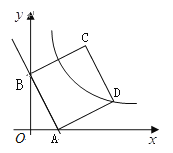
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A和B.
轴分别相交于点A和B.
(1)直接写出坐标:点A ,点B ;
(2)以线段AB为一边在第一象限内作□ABCD,其顶点D(![]() ,
, ![]() )在双曲线
)在双曲线![]() (
(![]() >
>![]() )上.
)上.
①求证:四边形ABCD是正方形;
②试探索:将正方形ABCD沿![]() 轴向左平移多少个单位长度时,点C恰好落在双曲线
轴向左平移多少个单位长度时,点C恰好落在双曲线![]() (
(![]() >
>![]() )上.
)上.
查看答案和解析>>
科目:初中数学 来源: 题型:
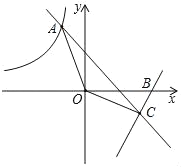
【题目】如图,直线y1=kx+2与反比例函数y2=![]() (x<0)相交于点A,且当x<﹣1时,y1>y2,当﹣1<x<0时,y1<y2.
(x<0)相交于点A,且当x<﹣1时,y1>y2,当﹣1<x<0时,y1<y2.
(1)求出y1的解析式;
(2)若直线y=2x+b与x轴交于点B(3,0),与y1交于点C,求出△AOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com