

分析 利用三角板角的特征和角平分线的定义解答,
(1)根据余角的定义即可得到结论;
(2)由角平分线的定义得到∠BOC=$\frac{1}{2}$∠COD=$\frac{1}{2}$×60°=30°,根据余角的定义即可得到结论;
(3)根据角平分线的定义得到$\frac{1}{2}$(∠BOD+∠AOC)=$\frac{1}{2}$×30°=15°,然后根据角的和差即可得到结果.
解答 解:(1)∠BOD=90°-60°=30°;
(2)∠BOC=$\frac{1}{2}$∠COD=$\frac{1}{2}$×60°=30°,
∴∠AOC=∠AOB-∠BOC=90°-30°=60°;
(3)∠BOD+∠AOC=90°-∠COD=90°-60°=30°,
$\frac{1}{2}$(∠BOD+∠AOC)=$\frac{1}{2}$×30°=15°,
∠MON=$\frac{1}{2}$(∠BOD+∠AOC)+∠COD=15°+60°75°
即∠MON的度数不会发生变化,总是75°.
点评 本题考查了角的计算:会进行角的倍、分、差计算.也考查了角平分线的定义,会识别图形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1+x)+15%(1+x)2=20% | B. | 15%(1+x%)2=20% | C. | 15%(1-x)2=20% | D. | 15%(1+x)2=20% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=3,OB=2,对角线AC、BD交于点G,若曲线y=$\frac{k}{x}$(x>0)经过点C、G,则k=$\frac{7}{2}$.
如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=3,OB=2,对角线AC、BD交于点G,若曲线y=$\frac{k}{x}$(x>0)经过点C、G,则k=$\frac{7}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
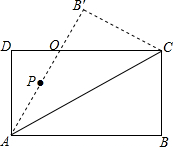 如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.
如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com