
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌжБЯп1ЗжБ№НЛ![]() жсЁЂ
жсЁЂ![]() жсгк
жсгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЕу
СНЕуЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎ
ЃЎ
(1)ЧѓжБЯп![]() ЕФНтЮіЪНМАЕу
ЕФНтЮіЪНМАЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
(2) Еу![]() дк
дк![]() жсЩЯДгЕу
жсЩЯДгЕу![]() ЯђЕу
ЯђЕу![]() вдУПУы1ИіЕЅЮЛГЄЕФЫйЖШдЫЖЏ(
вдУПУы1ИіЕЅЮЛГЄЕФЫйЖШдЫЖЏ(![]() )ЃЌЙ§Еу
)ЃЌЙ§Еу![]() ЗжБ№зї
ЗжБ№зї![]() ЃЌ
ЃЌ![]() ЃЌ НЛ
ЃЌ НЛ![]() ЁЂ
ЁЂ![]() гкЕу
гкЕу![]() ЁЂ
ЁЂ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
ЂйХаЖЯЫФБпаЮ![]() ЕФаЮзДВЂжЄУїЃЛ
ЕФаЮзДВЂжЄУїЃЛ
ЂкЧѓГіtЮЊКЮжЕЪБЯпЖЮDGЕФГЄзюЖЬЃЎ
(3)Еу![]() ЪЧ
ЪЧ![]() жсЩЯЕФЕуЃЌдкзјБъЦНУцФкЪЧЗёДцдкЕу
жсЩЯЕФЕуЃЌдкзјБъЦНУцФкЪЧЗёДцдкЕу![]() ЃЌЪЙвд
ЃЌЪЙвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЯюЕуЕФЫФБпаЮЪЧСтаЮ?ШєДцдкЃЌЧыжБНгаДГі
ЮЊЯюЕуЕФЫФБпаЮЪЧСтаЮ?ШєДцдкЃЌЧыжБНгаДГі![]() ЕуЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕуЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛ
ЃЛ![]() ЃЈ2ЃЉЂйОиаЮЃЛжЄУїМћНтЮіЂк
ЃЈ2ЃЉЂйОиаЮЃЛжЄУїМћНтЮіЂк![]() ЪБЃЌDGЕФГЄзюЖЬЃЈ3ЃЉДцдкЃЛ
ЪБЃЌDGЕФГЄзюЖЬЃЈ3ЃЉДцдкЃЛ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнгавЛИіНЧЮЊ30ЁуЕФжБНЧШ§НЧаЮЕФаджЪЃЌЧѓГіOBЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЂйИљОнгавЛИіНЧЪЧжБНЧЕФЦНааЫФБпаЮЪЧОиаЮЃЌХаЖЯГіЫФБпаЮDEBFЪЧОиаЮЃЛЂкРћгУЕуЕНжБЯпЕФОрРыжаДЙЯпЖЬзюЖЬМДПЩЃЛ
ЃЈ3ЃЉЩшГіЕуPЃЈ0ЃЌmЃЉЕФзјБъЃЌЯШРћгУЦНааЫФБпаЮЕФаджЪзїГіЭМаЮЃЌЧѓГіЕуQЕФзјБъЃЌдйРћгУСтаЮЕФЫФБпЯрЕШЧѓГіmМДПЩЃЎ
ЃЈ1ЃЉЁп![]() ЃЌ
ЃЌ
Ёр![]()
гжИљОнЬтвт![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]()
Ёр![]()
Щш![]() НтЮіЪНЮЊ
НтЮіЪНЮЊ![]()
ДњШы![]() ЃЌ
ЃЌ![]()
 ЕУ
ЕУ
Ёр![]() ЕФНтЮіЪНЃК
ЕФНтЮіЪНЃК![]()
Ёп![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌ
ЩЯЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃК
ЃК![]() ЃЌ
ЃЌ
ЁпЕуCдкxжсЩЯЃЌ
Ёр![]()
ЃЈ2ЃЉШчЭМЃК

ЂйЁп![]() ЃЌ
ЃЌ![]() ЃЌOA=1ЃЌ
ЃЌOA=1ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЈЙДЙЩЖЈРэЃЉЃЌ
ЃЈЙДЙЩЖЈРэЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ![]()
Ёр![]() ЃЌ
ЃЌ
гжЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЈСНзщЖдБпЗжБ№ЦНааЃЉЃЌ
ЪЧЦНааЫФБпаЮЃЈСНзщЖдБпЗжБ№ЦНааЃЉЃЌ
ЁрЫФБпаЮ![]() ЮЊОиаЮЃЈгавЛИіНЧЪЧ90ЁуЕФЦНааЫФБпаЮЪЧОиаЮЃЉЃЌ
ЮЊОиаЮЃЈгавЛИіНЧЪЧ90ЁуЕФЦНааЫФБпаЮЪЧОиаЮЃЉЃЌ
ЂкЁпЫФБпаЮ![]() ЮЊОиаЮ
ЮЊОиаЮ
Ёр![]() ЃЈОиаЮЖдНЧЯпЯрЕШЃЉЃЌ
ЃЈОиаЮЖдНЧЯпЯрЕШЃЉЃЌ
гжвђЮЊ![]() ЮЊ
ЮЊ![]() жаЕуЃЌ
жаЕуЃЌ
Ёр![]() ЃЌМДGЮЊОиаЮЖдНЧЯпЕФНЛЕуЃЌ
ЃЌМДGЮЊОиаЮЖдНЧЯпЕФНЛЕуЃЌ
вЊЪЙDGзюЖЬЃЌвВОЭЪЧDBзюЖЬЃЌ
ЁржЛгаBDЁЭACЪБЃЌBDзюЖЬЃЌ
ЁрCD=3ЃЌ
Ёр![]()
ЃЈ3ЃЉШчЭМ2ЃЌдкзјБъЦНУцФкЪЧДцдкЕуQЃЌЪЙвдAЁЂBЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃЌжЄУїШчЯТЃК

Щш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
ЁржБЯпABЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
зїaЁЮBPЃЌдђжБЯпaЕФНтЮіЪНЮЊЃКx=1ЃЌ
зїbЁЮAPЃЌдђжБЯпbЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
зїcЁЮBAЃЌдђжБЯпcЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
вд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЌдђ
ЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЌдђ![]() ЮЊЕШбќШ§НЧаЮ
ЮЊЕШбќШ§НЧаЮ
ЂйвдABЮЊЖдНЧЯпЪБЃЌга ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЫФБпаЮ![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ
Ёр![]() ЃЌМДЃК
ЃЌМДЃК![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
Ђк вдABЮЊБпЪБЃЌ
ЧщПі1ЃКAPЮЊЖдНЧЯпЪБЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ЁпABЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
APЕФНтЮіЪНЮЊЃК![]() Лђеп
Лђеп![]() ЃЌ
ЃЌ
ЁпЫФБпаЮAPQBЪЧСтаЮЃЌ
ЁрЕуQЙ§ЕуAЧвPQЁЮyжсЕФжБЯпЩЯЃЌ
Ёр![]() Лђеп
Лђеп![]() ЃЌ
ЃЌ
ЧщПі2ЃКвдBPЮЊЖдНЧЯпЪБЃЌ
Ёп![]()
ДЫЪБ![]() ЃЌ
ЃЌ
ЙЪДцдк4ЕуЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіГЄЮЊ4cmЃЌПэЮЊ3cmЕФГЄЗНаЮФОАхдкзРУцЩЯзіЮоЛЌЖЏЕФЗЙіЃЈЫГЪБеыЗНЯђЃЉЃЌФОАхЕуAЮЛжУЕФБфЛЏЮЊAЁњAlЁњA2ЃЌЦфжаЕкЖўДЮЗЙіБЛУцЩЯвЛаЁФОПщЕВзЁЃЌЪЙФОАхгызРУцГЩ30ЁуЕФНЧЃЌдђЕуAЙіЕНA2ЮЛжУЪБЙВзпЙ§ЕФТЗОЖГЄЮЊЃЈЁЁЁЁЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧыАбЯТСаЕФжЄУїЙ§ГЬВЙГфЭъећЃК

вбжЊ,ШчЭМ,BCEЁЂAFEЪЧжБЯп,ABЁЮCD,ЁЯ1=ЁЯ2,ЁЯ3=ЁЯ4,ЧѓжЄЃКADЁЮBE.
жЄУїЃКЁпABЁЮCD(вбжЊ)
ЁрЁЯ4=ЁЯ______
ЁпЁЯ3=ЁЯ4(вбжЊ)
ЁрЁЯ3=ЁЯ______(ЕШСПДњЛЛ)
ЁпЁЯ1=ЁЯ2(вбжЊ)
ЁрЁЯ1+ЁЯCAF=ЁЯ2+ЁЯCAF(ЕШЪНЕФаджЪ)
МДЁЯBAF=ЁЯ______
ЁрЁЯ3=ЁЯ______(ЕШСПДњЛЛ)
ЁрADЁЮBE______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБЯпy=Љkx+kЉ3гыжБЯпy=kxдкЭЌвЛзјБъЯЕжаЕФДѓжТЭМЯѓПЩФмЪЧЃЈЁЁЁЁЃЉ
A.  B.
B.  C.
C. 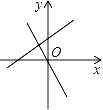 D.
D. 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§ЕФЭМЯѓЙ§M(1,3),N(-2,12)СНЕу.
(1)ЧѓКЏЪ§ЕФНтЮіЪН;
(2)ЪдХаЖЯЕуP(2a,-6a+8)ЪЧЗёдкКЏЪ§ЕФЭМЯѓЩЯ,ВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбСтаЮ![]() би
би![]() елЕўЃЌ
елЕўЃЌ![]() Тфдк
Тфдк![]() БпЩЯЕФ
БпЩЯЕФ![]() ДІЃЌШє
ДІЃЌШє![]() ЃЌдђ
ЃЌдђ![]() ЕФДѓаЁЮЊЃЈ ЃЉ
ЕФДѓаЁЮЊЃЈ ЃЉ

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФПЧАЮвЪаЁАаЃдАЪжЛњЁБЯжЯѓдНРДдНЪмЕНЩчЛсЙизЂЃЌеыЖдетжжЯжЯѓЃЌжиЧьвЛжаГѕШ§ЃЈ1ЃЉАрЪ§бЇаЫШЄаЁзщЕФЭЌбЇЫцЛњЕїВщСЫбЇаЃШєИЩУћМвГЄЖдЁАжабЇЩњДјЪжЛњЁБЯжЯѓЕФЬЌЖШЃЈЬЌЖШЗжЮЊЃКAЃЎЮоЫљЮНЃЛBЃЎЛљБОдоГЩЃЛCЃЎдоГЩЃЛDЃЎЗДЖдЃЉЃЌВЂНЋЕїВщНсЙћЛцжЦГЩЦЕЪ§елЯпЭГМЦЭМ1КЭЩШаЮЭГМЦЭМ2ЃЈВЛЭъећЃЉЃЎЧыИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉДЫДЮГщбљЕїВщжаЃЌЙВЕїВщСЫЖрЩйУћжабЇЩњМвГЄЃЛ
ЃЈ2ЃЉЧѓГіЭМ2жаЩШаЮCЫљЖдЕФдВаФНЧЕФЖШЪ§ЃЌВЂНЋЭМ1ВЙГфЭъећЃЛ
ЃЈ3ЃЉИљОнГщбљЕїВщНсЙћЃЌЧыФуЙРМЦЮваЃ11000УћжабЇЩњМвГЄжагаЖрЩйУћМвГЄГжЗДЖдЬЌЖШЃЛ
ЃЈ4ЃЉдкДЫДЮЕїВщЛюЖЏжаЃЌГѕШ§ЃЈ1ЃЉАрКЭГѕШ§ЃЈ2ЃЉАрИїга2ЮЛМвГЄЖджабЇЩњДјЪжЛњГжЗДЖдЬЌЖШЃЌЯжДгжабЁ2ЮЛМвГЄВЮМгбЇаЃзщжЏЕФМваЃЛюЖЏЃЌгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЧѓбЁГіЕФ2ШЫРДздВЛЭЌАрМЖЕФИХТЪЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЯпЃЌ
ЕФжаЯпЃЌ![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() .
.
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЛ
ЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШєЫФБпаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧыжБНгаДГіЭМжаЫљгаУцЛ§ЪЧ
ЃЌЧыжБНгаДГіЭМжаЫљгаУцЛ§ЪЧ![]() ЕФШ§НЧаЮ.
ЕФШ§НЧаЮ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌЕуCдкЯпЖЮABЩЯЃЌЧвAC=6cmЃЌBC=14cmЃЌЕуMЁЂNЗжБ№ЪЧACЁЂBCЕФжаЕуЃЎ
![]()
ЃЈ1ЃЉЧѓЯпЖЮMNЕФГЄЖШЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉжаЃЌШчЙћAC=acmЃЌBC=bcmЃЌЦфЫќЬѕМўВЛБфЃЌФуФмВТВтГіMNЕФГЄЖШТ№ЃПЧыЫЕГіФуЗЂЯжЕФНсТлЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com