
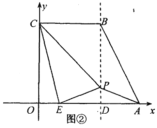
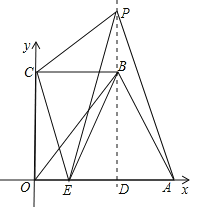
【题目】如图①,将直角梯形![]() 放在平面直角坐标系中,已知
放在平面直角坐标系中,已知![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,连结
,连结![]() .
.

(1)求证:![]() ;
;
(2)如图②,过点![]() 作
作![]() 轴于
轴于![]() ,点
,点![]() 在直线
在直线![]() 上运动,连结
上运动,连结![]() 和
和![]() .
.
①当![]() 的周长最短时,求点
的周长最短时,求点![]() 的坐标;
的坐标;
②如果点![]() 在
在![]() 轴上方,且满足
轴上方,且满足![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)①![]() ;②
;②![]() 或8
或8
【解析】
(1)先由已知条件及勾股定理求出AE=4,AB=![]() ,得到
,得到![]() ,又∠OAB=∠BAE,根据两边对应成比例且夹角相等的两三角形相似证明△OAB∽△BAE,得出∠AOB=∠ABE,再由两直线平行,内错角相等得出∠OBC=∠AOB,从而证明∠OBC=∠ABE;
,又∠OAB=∠BAE,根据两边对应成比例且夹角相等的两三角形相似证明△OAB∽△BAE,得出∠AOB=∠ABE,再由两直线平行,内错角相等得出∠OBC=∠AOB,从而证明∠OBC=∠ABE;
(2)①由于CE为定长,所以当PC+PE最短时,△PCE的周长最短,而E与A关于BD对称,故连接AC,交BD于P,即当点C、P、A三点共线时,△PCE的周长最短.由PD∥OC,得出![]() ,求出PD的值,从而得到点P的坐标;
,求出PD的值,从而得到点P的坐标;
②由于点P在x轴上方,BD=4,所以分两种情况:0<PD≤4与PD>4.设PD=t,先用含t的代数式分别表示S△CEP与S△ABP,再根据S△CEP:S△ABP=2:1,即可求出DP的长.
解:(1)由题意可得:
∵OC=4,BC=3,∠OCB=90°,
∴OB=5.
∵OA=5,OE=1,
∴AE=4,AB=![]() ,
,
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)①∵BD⊥x轴,ED=AD=2,
∴E与A关于BD对称,
当点![]() 共线时,
共线时,![]() 的周长最短.
的周长最短.
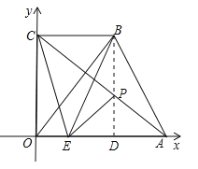
∵![]() ,
,
∴![]() ,即
,即![]()
∴![]()
∴![]() .
.
②设![]() ,
,
当![]() 时,如图:
时,如图:
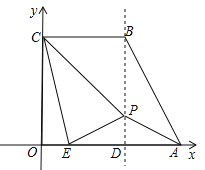
∵![]() 梯
梯![]()
![]() ,
,
![]() ;
;
又∵![]() .
.
∴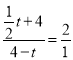 ,
,
∴![]() ;
;
当![]() 时,如图:
时,如图:
∵![]() ,
,![]() ,
,
∴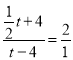
![]() .
.
![]() .
.
∴所求DP的长为![]() 或8.
或8.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10![]() cm,且tan∠EFC=
cm,且tan∠EFC=![]() ,那么该矩形的周长为( )
,那么该矩形的周长为( )
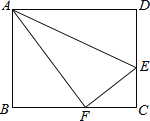
A. 72cm B. 36cm C. 20cm D. 16cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,点O是AC上一动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.

⑴说明:OE=OF
⑵当点O运动到何处时,四边形AECF是矩形,证明你的结论
⑶在⑵的条件下,当⊿ABC满足什么条件时,四边形AECF为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班委会决定,选购圆珠笔、钢笔共22支,送给山区学校的同学。已知圆珠笔每支5元,钢笔每支6元。
(1)若购买圆珠笔、钢笔刚好用去120元,问圆珠笔、钢笔各买了多少支?
(2)若购圆珠笔可9折优惠,钢笔可8折优惠,在所需费用不超过100元的前提下,请你写出一种选购方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
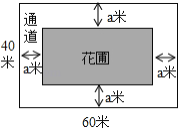
(1)当a=10米时,花圃的面积=
(2)通道的面积与花圃的面积之比能否恰好等于3:5,如果可以,求出此时通道的宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ;这两个图象交于
;这两个图象交于![]() 轴上一点
轴上一点![]() ,直线
,直线![]() 与
与![]() 轴的交点
轴的交点![]() 动点
动点![]() 从点
从点![]() 出发沿
出发沿![]() 轴以每秒1个单位长的速度向左移动,设移动时间为
轴以每秒1个单位长的速度向左移动,设移动时间为![]() 秒,当
秒,当![]() __________时,
__________时,![]() 为等腰三角形.
为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上依次有A,C,B三地,甲、乙两人同时出发,甲从A地骑自行车去B地,途经C地休息1分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行从B地前往A地.甲、乙两人距A地的路程y(米)与时间x(分)之间的函数关系如图所示,请结合图象解答下列问题:
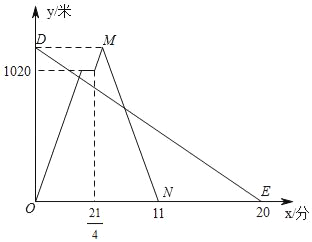
(1)请写出甲的骑行速度为 米/分,点M的坐标为 ;
(2)求甲返回时距A地的路程y与时间x之间的函数关系式(不需要写出自变量的取值范围);
(3)请直接写出两人出发后,在甲返回A地之前,经过多长时间两人距C地的路程相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中.AC=BC=5.AB=6.CD是AB边中线.点P从点C出发,以每秒2.5个单位长度的速度沿C-D-C运动.在点P出发的同时,点Q也从点C出发,以每秒2个单位长度的速度沿边CA向点A运动.当一个点停止运动时,另一个点也随之停止,设点P运动的时间为t秒.
(1)用含t的代数式表示CP、CQ的长度.
(2)用含t的代数式表示△CPQ的面积.
(3)当△CPQ与△CAD相似时,直接写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com