
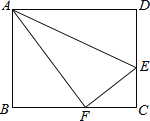
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10![]() cm,且tan∠EFC=
cm,且tan∠EFC=![]() ,那么该矩形的周长为( )
,那么该矩形的周长为( )
A. 72cm B. 36cm C. 20cm D. 16cm
【答案】A
【解析】
在矩形ABCD中,AB=CD,AD=BC,∠B=∠D=90°,
∵△ADE沿AE对折,点D的对称点F恰好落在BC上,∴∠AFE=∠D=90°,AD=AF。
∵∠EFC+∠AFB=180°﹣90°=90°,∠BAF+∠AFB=90°,∴∠BAF=∠EFC。
∵tan∠EFC=![]() ,∴tan∠BAF =
,∴tan∠BAF =![]() 。∴设BF=3x、AB=4x。
。∴设BF=3x、AB=4x。
在Rt△ABF中,根据勾股定理可得AF=5x,∴AD=BC=5x。∴CF=BC﹣BF=5x﹣3x=2x。
∵tan∠EFC=![]() ,∴CE=CFtan∠EFC=2x
,∴CE=CFtan∠EFC=2x![]() =
=![]() x。∴DE=CD﹣CE=4x﹣
x。∴DE=CD﹣CE=4x﹣![]() x=
x=![]() x。
x。
在Rt△ADE中,AD2+DE2=AE2,即(5x)2+(![]() x)2=(10
x)2=(10![]() )2,整理得,x2=16,解得x=4。
)2,整理得,x2=16,解得x=4。
∴AB=4×4=16cm,AD=5×4=20cm,矩形的周长=2(16+20)=72cm。故选A。


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
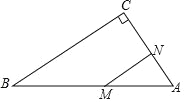
【题目】如图,在 Rt△ABC 中,∠C=90°,∠A=60°,AB=10cm,若点M 从点 B 出发以 2cm/s 的速度向点 A 运动,点 N 从点 A 出发以 1cm/s 的速度向点 C 运动,设 M、N 分别从点 B、A 同时出发,运动的时间为 ts.
(1)用含 t 的式子表示线段 AM、AN 的长;
(2)当 t 为何值时,△AMN 是以 MN 为底边的等腰三角形?
(3)当 t 为何值时,MN∥BC?并求出此时 CN 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D,E,F分别是AC,AB,BC的中点.点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点G.点P,Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
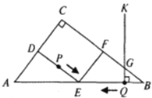
(1)D,F两点间的距离是 ;
(2)射线QK能否把四边形CDEF分成面积相等的两部分?若能,求出t的值.若不能,说明理由;
(3)当点P运动到折线EF-FC上,且点P又恰好落在射线QK上时,求t的值;
(4)连结PG,当PG∥AB时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知在△ABC中,∠B=90°,AB=6cm,BC=12cm,点Q从点A开始沿AB边向点B以1cm/s的速度移动,点P从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果Q、P分别从A、B两点出发,那么几秒后,△PBQ的面积等于8cm2?
(2)在(1)中,△PBQ的面积能否等于10cm2?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
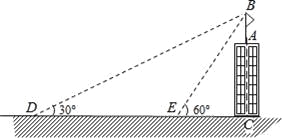
【题目】如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41.
≈1.41.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国魏晋时期数学家刘徽编撰的最早一部测量数学著作《海岛算经》中有一题:今有望海岛,立两表齐高三丈,前后相去千步,令后表与前表参相直.从前表却行一百二十三步,人目着地,取望岛峰,与表末参合.从后表却行一百二十七步,人目着地,取望岛峰,亦与表末参合.问岛高几何?

译文:今要测量海岛上一座山峰AH的高度,在B处和D处树立标杆BC和DE,标杆的高都是3丈,B和D两处相隔1000步(1丈=10尺,1步=6尺),并且AH,CB和DE在同一平面内.从标杆BC后退123步的F处可以看到顶峰A和标杆顶端C在同一直线上;从标杆ED后退127步的G处可以看到顶峰A和标杆顶端E在同一直线上.则山峰AH的高度是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程x2+kx﹣3=0的一个根是x=1,则另一个根是___.
【答案】-3.
【解析】
解:∵x=1是一元二次方程的根,∴12+k×1-3=0,∴k=2,∴x2+2x-3=0,∴(x+3)(x-1)=0,∴x1=-3,x2=1.故答案为:-3.
【题型】填空题
【结束】
19
【题目】如图,在△ABC中,AB=8,AC=6,AD=12,点D在BC的延长线上,且△ACD∽△BAD,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将直角梯形![]() 放在平面直角坐标系中,已知
放在平面直角坐标系中,已知![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,连结
,连结![]() .
.

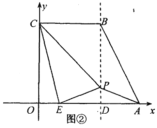
(1)求证:![]() ;
;
(2)如图②,过点![]() 作
作![]() 轴于
轴于![]() ,点
,点![]() 在直线
在直线![]() 上运动,连结
上运动,连结![]() 和
和![]() .
.
①当![]() 的周长最短时,求点
的周长最短时,求点![]() 的坐标;
的坐标;
②如果点![]() 在
在![]() 轴上方,且满足
轴上方,且满足![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com