
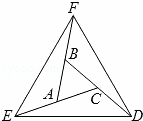
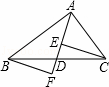
已知,如图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接D,E,F,得到△DEF为等边三角形.求证:
(1)△AEF≌△CDE;
(2)△ABC为等边三角形.
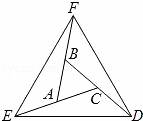
证明:(1)∵BF=AC,AB=AE(已知)
∴FA=EC(等量加等量和相等).
∵△DEF是等边三角形(已知),
∴EF=DE(等边三角形的性质).
又∵AE=CD(已知),
∴△AEF≌△CDE(SSS).
(2)由△AEF≌△CDE,得∠FEA=∠EDC(对应角相等),
∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF(等量代换),
△DEF是等边三角形(已知),
∴∠DEF=60°(等边三角形的性质),
∴∠BCA=60°(等量代换),
由△AEF≌△CDE,得∠EFA=∠DEC,
∵∠DEC+∠FEC=60°,
∴∠EFA+∠FEC=60°,
又∠BAC是△AEF的外角,
∴∠BAC=∠EFA+∠FEC=60°,
∴△ABC中,AB=BC(等角对等边).
∴△ABC是等边三角形(等边三角形的判定).


科目:初中数学 来源: 题型:
小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况. 他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
| 分组 | 频数 | 百分比 |
| 600≤ | 2 | 5% |
| 800≤ | 6 | 15% |
| 1000≤ | 45% | |
| 9 | 22.5% | |
| 1600≤ | 2 | |
| 合计 | 40 | 100% |
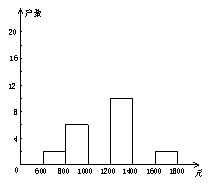
根据以上提供的信息,解答下列问题:(1)补全频数分布表.(2)补全频数分布直方图.(3)绘制相应的频数分布折线图.(4)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
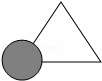
A. SSS B. SAS C. AAS D. ASA
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE、下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com