练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    设三角形的三边长分别等于下列各组数，能构成直角三角形的是(     )

    A．1，2，3   B．4，5，6   C．6，8，10 D．7，12，13


    C【考点】勾股数．

    【分析】判断是否可以作为直角三角形的三边长，则判断两小边的平方和是否等于最长边的平方即可．

    【解答】解：A、12+22≠32，不是直角三角形，故此选项错误；

    B、42+52≠62，不是直角三角形，故此选项错误；

    C、62+82=102，是直角三角形，故此选项正确；

    D、72+122≠132，不是直角三角形，故此选项错误．

    故选：C．

    【点评】此题主要考查了勾股定理逆定理，关键是掌握勾股定理的逆定理：已知△ABC的三边满足a2+b2=c2，则△ABC是直角三角形．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形，如果所剪得的两个正方形边长都是1，那么圆形纸片和扇形纸片的面积比是(     )

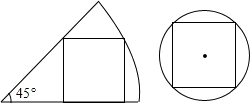
    A．4：5 B．2：5  C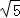．：2     D．：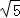

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某商场购进一种单价为40元的篮球，如果以单价50元出售，那么每月可售出500个，根据销售经验，售价每提高1元，销售量相应减少10个；

    （1）假设销售单价提高x元，那么销售每个篮球所获得的利润是__________元；这种篮球每月的销售量是__________个；（用含x的代数式表示）

    （2）若商店准备获利8000元，则销售定价为多少元？商店应进货多少个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AC∥CD，点E在BC上，若∠D=∠DEC=74°，求∠B的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    海面上的A，B，C三艘船的平面图如图所示，C船在A船的北偏东55°方向，B船在A船的北偏东85°方向，C船在B船的北偏西25°方向．

    （1）从B船看A，C两船的视角∠ABC是多少度？

    （2）从C船看A，B两船的视角∠ACB是多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图将4个长、宽分别均为a，b的长方形，摆成了一个大的正方形，利用面积的不同表示方法写出一个代数恒等式是(     )

    A．a2+2ab+b2=（a+b）2      B．a2﹣2ab+b2=（a﹣b）2

    C．4ab=（a+b）2﹣（a﹣b）2    D．（a+b）（a﹣b）=a2﹣b2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC中，AB+AC=6cm，BC的垂直平分线l与AC相交于点D，则△ABD的周长为__________cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    王刚同学在解关于x的方程x2﹣3x+c=0时，误将﹣3x看作+3x，结果解得x1=1，x2=﹣4，则原方程的解为（　　）

    A．x1=﹣1，x2=﹣4    B．x1=1，x2=4    C．x1=﹣1，x2=4  D．x1=2，x2=3

    查看答案和解析>>

    科目：初中数学 来源： 题型：



    如图所示，图①②③④均为直角三角形．根据图中数据完成（1）填空，并按要求续作（2）（3）：

    （1）sin2A1+sin2B1=　 　；sin2A2+sin2B2=　 　；sin2A3+sin2B3=　 　．猜想：在Rt△ABC中，∠C=90°，都有sin2A+sin2B=　 　．

    （2）如图④，在Rt△ABC中，∠C=90°，∠A、∠B、∠C的对边分别是a、b、c，利用锐角三角比的定义和勾股定理，证明你的猜想．

    （3）已知：∠A+∠B=90°，且sinA=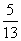求sinB．

    查看答案和解析>>

    同步练习册答案