
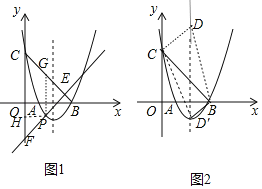
°Њћвƒњ°њ»зЌЉ£ђ≈„ќпѕяy=x2+bx+c”лx÷бљї”ЏA°ҐBЅљµг£ђBµг„ш±кќ™£®4£ђ0£©£ђ”лy÷бљї”ЏµгC£®0£ђ4£©£Ѓ
£®1£©«у≈„ќпѕяµƒљвќц љ£ї
£®2£©µгP‘Џx÷бѕ¬Јљµƒ≈„ќпѕя…ѕ£ђєэµгPµƒ÷±ѕяy=x+m”л÷±ѕяBCљї”ЏµгE£ђ”лy÷бљї”ЏµгF£ђ«уPE+EFµƒ„оіу÷µ£ї
£®3£©µгDќ™≈„ќпѕяґ‘≥∆÷б…ѕ“їµг£Ѓ
Ґўµ±°чBCD «“‘BCќ™÷±љ«±яµƒ÷±љ«»эљ«–ќ ±£ђ÷±љ”–і≥цµгDµƒ„ш±к£ї
ҐЏ»ф°чBCD «»сљ«»эљ«–ќ£ђ÷±љ”–і≥цµгDµƒ„Ё„ш±кnµƒ»°÷µЈґќІ£Ѓ

°Њір∞Є°њ£®1£©≈„ќпѕяµƒљвќц љќ™y=x2©Б5x+4£ї£®2£©PE+EFµƒ„оіу÷µќ™![]() £ї£®3£©ҐўЈыЇѕћхЉюµƒµгDµƒ„ш±к «£®
£ї£®3£©ҐўЈыЇѕћхЉюµƒµгDµƒ„ш±к «£®![]() £ђ
£ђ![]() £©їт£®
£©їт£®![]() £ђ©Б
£ђ©Б![]() £©£їҐЏµгDµƒ„Ё„ш±кµƒ»°÷µЈґќІќ™
£©£їҐЏµгDµƒ„Ё„ш±кµƒ»°÷µЈґќІќ™![]() £Љy£Љ
£Љy£Љ![]() їт©Б
їт©Б![]() £Љy£Љ
£Љy£Љ![]() £Ѓ
£Ѓ
°Њљвќц°њ£®1£©јы”√іэґ®ѕµ эЈ®«у≈„ќпѕяµƒљвќц љ£ї
£®2£©“„µ√BCµƒљвќц љќ™y=©Бx+4£ђѕ»÷§√ч°чECFќ™µ»—ь÷±љ«»эљ«–ќ£ђ„чPH°Ќy÷б”ЏH£ђPG°ќy÷бљїBC”ЏG£ђ»зЌЉ1£ђ‘т°чEPGќ™µ»—ь÷±љ«»эљ«–ќ£ђPE=![]() PG£ђ…иP£®t£ђt2©Б4t+3£©£®1£Љt£Љ3£©£ђ‘тG£®t£ђ©Бt+3£©£ђљ”„≈јы”√t±н ЊPF°ҐPE£ђЋщ“‘PE+EF=2PE+PF=©Б
PG£ђ…иP£®t£ђt2©Б4t+3£©£®1£Љt£Љ3£©£ђ‘тG£®t£ђ©Бt+3£©£ђљ”„≈јы”√t±н ЊPF°ҐPE£ђЋщ“‘PE+EF=2PE+PF=©Б![]() t2+5
t2+5![]() t£ђ»їЇујы”√ґюіќЇѓ эµƒ–‘÷ љвЊцќ ћв£ї
t£ђ»їЇујы”√ґюіќЇѓ эµƒ–‘÷ љвЊцќ ћв£ї
£®3£©Ґў»зЌЉ2£ђ≈„ќпѕяµƒґ‘≥∆÷бќ™÷±ѕяx=©БµгDµƒ„Ё„ш±кµƒ»°÷µЈґќІ£ї
ҐЏ”…”Џ°чBCD «“‘BCќ™–±±яµƒ÷±љ«»эљ«–ќ”–4+£®y©Б3£©2+1+y2=18£ђљвµ√y1=![]() £ђy2=
£ђy2=![]() £ђµ√µљіЋ ±Dµг„ш±кќ™£®
£ђµ√µљіЋ ±Dµг„ш±кќ™£®![]() £ђ
£ђ![]() £©їт£®
£©їт£®![]() £ђ
£ђ![]() £©£ђ»їЇуљбЇѕЌЉ–ќњ…»Јґ®°чBCD «»сљ«»эљ«–ќ ±µгDµƒ„Ё„ш±кµƒ»°÷µЈґќІ£Ѓ
£©£ђ»їЇуљбЇѕЌЉ–ќњ…»Јґ®°чBCD «»сљ«»эљ«–ќ ±µгDµƒ„Ё„ш±кµƒ»°÷µЈґќІ£Ѓ
£®1£©∞—B£®4£ђ0£©£ђC£®0£ђ4£©іъ»лy=x2+bx+c£ђµ√
![]() £ђ
£ђ
љвµ√ ![]() £ђ
£ђ
°а≈„ќпѕяµƒљвќц љќ™y=x2©Б5x+4£ї
£®2£©”…B£®4£ђ0£©£ђC£®0£ђ4£©£ђЄщЊЁіэґ®ѕµ эЈ®“„µ√BCµƒљвќц љќ™y=©Бx+4£ђ
°я÷±ѕяy=x+m”л÷±ѕяy=x∆љ––£ђ
°а÷±ѕяy=©Бx+4”л÷±ѕяy=x+mіє÷±£ђ
°а°ѕCEF=90°г£ђ
°а°чECFќ™µ»—ь÷±љ«»эљ«–ќ£ђ
„чPH°Ќy÷б”ЏH£ђPG°ќy÷бљїBC”ЏG£ђ»зЌЉ1£ђ°чEPGќ™µ»—ь÷±љ«»эљ«–ќ£ђPE=![]() PG£ђ
PG£ђ
…иP£®t£ђt2©Б5t+4£©£®1£Љt£Љ4£©£ђ‘тG£®t£ђ©Бt+4£©£ђ
°аPF=![]() PH=
PH=![]() t£ђPG=©Бt+4©Б£®t2©Б5t+4£©=©Бt2+4t£ђ
t£ђPG=©Бt+4©Б£®t2©Б5t+4£©=©Бt2+4t£ђ
°аPE=![]() PG=©Б
PG=©Б![]() t2+2
t2+2![]() t£ђ
t£ђ
°аPE+EF=PE+PE+PF=2PE+PF=©Б![]() t2+4
t2+4![]() t+
t+![]() t=©Б
t=©Б![]() t2+5
t2+5![]() t=©Б
t=©Б![]() £®t©Б
£®t©Б![]() £©2+
£©2+![]() £ђ
£ђ
µ±t=![]() ±£ђPE+EFµƒ„оіу÷µќ™
±£ђPE+EFµƒ„оіу÷µќ™![]() £ї
£ї
£®3£©Ґў»зЌЉ2£ђ≈„ќпѕяµƒґ‘≥∆÷бќ™÷±ѕяx=![]() £ђ
£ђ
…иD£®![]() £ђy£©£ђ‘тBC2=42+42=32£ђDC2=£®
£ђy£©£ђ‘тBC2=42+42=32£ђDC2=£®![]() £©2+£®y©Б4£©2£ђBD2=£®4©Б
£©2+£®y©Б4£©2£ђBD2=£®4©Б![]() £©2+y2=
£©2+y2=![]() +y2£ђ
+y2£ђ
µ±°чBCD «“‘BCќ™÷±љ«±я£ђBDќ™–±±яµƒ÷±љ«»эљ«–ќ ±£ђBC2+DC2=BD2£ђ
Љі32+£®![]() £©2+£®y©Б4£©2=
£©2+£®y©Б4£©2=![]() +y2£ђљвµ√y=5£ђіЋ ±Dµг„ш±кќ™£®
+y2£ђљвµ√y=5£ђіЋ ±Dµг„ш±кќ™£®![]() £ђ
£ђ![]() £©£ї
£©£ї
µ±°чBCD «“‘BCќ™÷±љ«±я£ђCDќ™–±±яµƒ÷±љ«»эљ«–ќ ±£ђBC2+DB2=DC2£ђ
Љі32+![]() +y2=£®
+y2=£®![]() £©2+£®y©Б4£©2£ђљвµ√y=©Б1£ђіЋ ±Dµг„ш±кќ™£®
£©2+£®y©Б4£©2£ђљвµ√y=©Б1£ђіЋ ±Dµг„ш±кќ™£®![]() £ђ©Б
£ђ©Б![]() £©£ї
£©£ї
„џ…ѕЋщ ц£ђЈыЇѕћхЉюµƒµгDµƒ„ш±к «£®![]() £ђ
£ђ![]() £©їт£®
£©їт£®![]() £ђ©Б
£ђ©Б![]() £©£ї
£©£ї
ҐЏµ±°чBCD «“‘BCќ™–±±яµƒ÷±љ«»эљ«–ќ ±£ђDC2+DB2=BC2£ђЉі£®![]() £©2+£®y©Б4£©2+
£©2+£®y©Б4£©2+![]() +y2=32£ђљвµ√y1=
+y2=32£ђљвµ√y1=![]() £ђy2=
£ђy2=![]() £ђіЋ ±Dµг„ш±кќ™£®
£ђіЋ ±Dµг„ш±кќ™£®![]() £ђ
£ђ![]() £©їт£®
£©їт£®![]() £ђ
£ђ![]() £©£ђ
£©£ђ
Ћщ“‘°чBCD «»сљ«»эљ«–ќ£ђµгDµƒ„Ё„ш±кµƒ»°÷µЈґќІќ™![]() £Љy£Љ
£Љy£Љ![]() їт©Б
їт©Б![]() £Љy£Љ
£Љy£Љ![]() £Ѓ
£Ѓ


 «бЋ…њќћ√µ•‘™∆Џ÷–∆Џƒ©„®ћв≥еіћ100Ј÷ѕµЅ–ір∞Є
«бЋ…њќћ√µ•‘™∆Џ÷–∆Џƒ©„®ћв≥еіћ100Ј÷ѕµЅ–ір∞Є
| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“їЌжЊя≥І»•ƒк…ъ≤ъƒ≥÷÷ЌжЊя£ђ≥…±Њќ™![]() ‘™/Љю£ђ≥ц≥ІЉџќ™
‘™/Љю£ђ≥ц≥ІЉџќ™![]() ‘™/Љю£ђƒкѕъ џЅњќ™
‘™/Љю£ђƒкѕъ џЅњќ™![]() ЌтЉю£ЃљсƒкЉ∆їЃЌ®єэ µ±‘цЉ”≥…±ЊјіћбЄя≤ъ∆Јµµіќ£ђ“‘ЌЎ’є –≥°£Ѓ»фљсƒк’в÷÷ЌжЊя√њЉюµƒ≥…±Њ±»»•ƒк≥…±Њ‘цЉ”
ЌтЉю£ЃљсƒкЉ∆їЃЌ®єэ µ±‘цЉ”≥…±ЊјіћбЄя≤ъ∆Јµµіќ£ђ“‘ЌЎ’є –≥°£Ѓ»фљсƒк’в÷÷ЌжЊя√њЉюµƒ≥…±Њ±»»•ƒк≥…±Њ‘цЉ”![]() ±ґ£ђљсƒк’в÷÷ЌжЊя√њЉюµƒ≥ц≥ІЉџ±»»•ƒк≥ц≥ІЉџѕа”¶ћбЄя
±ґ£ђљсƒк’в÷÷ЌжЊя√њЉюµƒ≥ц≥ІЉџ±»»•ƒк≥ц≥ІЉџѕа”¶ћбЄя![]() ±ґ£ђ‘т‘§Љ∆љсƒкƒкѕъ џЅњљЂ±»»•ƒкƒкѕъ џЅњ‘цЉ”
±ґ£ђ‘т‘§Љ∆љсƒкƒкѕъ џЅњљЂ±»»•ƒкƒкѕъ џЅњ‘цЉ”![]() ±ґ£®±Њћв÷–
±ґ£®±Њћв÷–![]() £©£Ѓ
£©£Ѓ
![]() ”√Їђ
”√Їђ![]() µƒіъ э љ±н Њ£ђљсƒк…ъ≤ъµƒ’в÷÷ЌжЊя√њЉюµƒ≥…±Њќ™________‘™£ђљсƒк…ъ≤ъµƒ’в÷÷ЌжЊя√њЉюµƒ≥ц≥ІЉџќ™________‘™£Ѓ
µƒіъ э љ±н Њ£ђљсƒк…ъ≤ъµƒ’в÷÷ЌжЊя√њЉюµƒ≥…±Њќ™________‘™£ђљсƒк…ъ≤ъµƒ’в÷÷ЌжЊя√њЉюµƒ≥ц≥ІЉџќ™________‘™£Ѓ
![]() «уљсƒк’в÷÷ЌжЊяµƒ√њЉюјы»у
«уљсƒк’в÷÷ЌжЊяµƒ√њЉюјы»у![]() ‘™”л
‘™”л![]() ÷ЃЉдµƒЇѓ эєЎѕµ љ£Ѓ
÷ЃЉдµƒЇѓ эєЎѕµ љ£Ѓ
![]() …иљсƒк’в÷÷ЌжЊяµƒƒкѕъ џјы»уќ™
…иљсƒк’в÷÷ЌжЊяµƒƒкѕъ џјы»уќ™![]() Ќт‘™£ђ«уµ±
Ќт‘™£ђ«уµ±![]() ќ™Їќ÷µ ±£ђљсƒкµƒƒкѕъ џјы»у„оіу£њ„оіуƒкѕъ џјы»у «ґа…ўЌт‘™£њ
ќ™Їќ÷µ ±£ђљсƒкµƒƒкѕъ џјы»у„оіу£њ„оіуƒкѕъ џјы»у «ґа…ўЌт‘™£њ
„Ґ£Їƒкѕъ џјы»у![]() £®√њЉюЌжЊяµƒ≥ц≥ІЉџ-√њЉюЌжЊяµƒ≥…±Њ£©
£®√њЉюЌжЊяµƒ≥ц≥ІЉџ-√њЉюЌжЊяµƒ≥…±Њ£©![]() ƒкѕъ џЅњ£Ѓ
ƒкѕъ џЅњ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђЊЎ–ќ÷љ∆ђABCD÷–£ђ“—÷™AD =8£ђ’џµю÷љ∆ђ єAB±я”лґ‘љ«ѕяAC
÷ЎЇѕ£ђµгB¬д‘ЏµгFі¶£ђ’џЇџќ™AE£ђ«“EF=3£ђ‘тABµƒ≥§ќ™( )

A. 3 B. 4
C. 5 D. 6
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђAD°ќBC£ђ°ѕBAD£љ90°г£ђ“‘µгBќ™‘≤–ƒ£ђBC≥§ќ™∞лЊґї≠ї°£ђ”л…дѕяADѕаљї”ЏµгE£ђЅђљбBE£ђєэCµг„чCF°ЌBE£ђіє„гќ™F£Ѓ
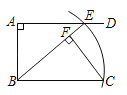
£®1£©ѕяґќBF”лЌЉ÷–ѕ÷”–µƒƒƒ“їћхѕяґќѕаµ»£њѕ»љЂƒг≤¬ѕл≥цµƒљб¬џћо–і‘Џѕ¬√жµƒЇбѕя…ѕ£ђ»їЇу‘ўЉ”“‘÷§√ч£Ѓ
љб¬џ£ЇBF£љ°° °°£ї
£®2£©»фAB£љ6£ђAE£љ8£ђ«уµгAµљµгCµƒЊајл£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ‘Џ![]() ÷–£ђ
÷–£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() √жїэќ™10£ђ
√жїэќ™10£ђ![]() µƒіє÷±∆љЈ÷ѕя
µƒіє÷±∆љЈ÷ѕя![]() Ј÷±рљї
Ј÷±рљї![]() £ђ
£ђ![]() ”Џµг
”Џµг![]() £ђ
£ђ![]() °£»фµг
°£»фµг![]() ќ™
ќ™![]() µƒ÷–µг£ђµг
µƒ÷–µг£ђµг![]() ќ™ѕяґќ
ќ™ѕяґќ![]() …ѕ“їґѓµг£ђ‘т
…ѕ“їґѓµг£ђ‘т![]() ÷№≥§µƒ„о–°÷µќ™______°£
÷№≥§µƒ„о–°÷µќ™______°£
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
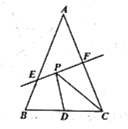
°Њћвƒњ°њ»зЌЉЋщ Њ£ђ–°√чЉ“–°«шњ’µЎ…ѕ”–Ѕљњ√± ÷±µƒ ч![]() °Ґ
°Ґ![]() £Ѓ“їћм£ђЋы‘Џ
£Ѓ“їћм£ђЋы‘Џ![]() і¶≤вµ√ чґ•
і¶≤вµ√ чґ•![]() µƒ—цљ«
µƒ—цљ«![]() £ђ‘Џ
£ђ‘Џ![]() і¶≤вµ√ чґ•
і¶≤вµ√ чґ•![]() µƒ—цљ«
µƒ—цљ«![]() £ђѕяґќ
£ђѕяґќ![]() «°Ї√Њ≠єэ чґ•
«°Ї√Њ≠єэ чґ•![]() £Ѓ“—÷™
£Ѓ“—÷™![]() °Ґ
°Ґ![]() Ѕљі¶µƒЊајлќ™
Ѕљі¶µƒЊајлќ™![]() √„£ђЅљњ√ ч÷ЃЉдµƒЊајл
√„£ђЅљњ√ ч÷ЃЉдµƒЊајл![]() √„£ђ
√„£ђ![]() °Ґ
°Ґ![]() °Ґ
°Ґ![]() °Ґ
°Ґ![]() Ћƒµг£Ѓ‘Џ“їћх÷±ѕя…ѕ£ђ«у ч
Ћƒµг£Ѓ‘Џ“їћх÷±ѕя…ѕ£ђ«у ч![]() µƒЄяґ»£Ѓ£®љбєыЊЂ»Јµљ
µƒЄяґ»£Ѓ£®љбєыЊЂ»Јµљ![]() √„£ђ≤ќњЉ эЊЁ£Ї
√„£ђ≤ќњЉ эЊЁ£Ї![]() £ђ
£ђ![]() £ђ
£ђ![]() £Ѓ£©
£Ѓ£©

≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ![]() ÷–£ђ
÷–£ђ![]() £ђµг
£ђµг![]() °Ґ
°Ґ![]() Ј÷±рќ™
Ј÷±рќ™![]() µƒЌв–ƒЇЌƒЏ–ƒ£ђ
µƒЌв–ƒЇЌƒЏ–ƒ£ђ![]() £ђ
£ђ![]() £ђ‘т
£ђ‘т![]() µƒ÷µќ™£® £©
µƒ÷µќ™£® £©

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™£ђ»зЌЉ1£ђ‘ЏABCD÷–£ђµгE «AB÷–µг£ђЅђљ”DE≤Ґ—”≥§£ђљїCBµƒ—”≥§ѕя”ЏµгF£Ѓ
£®1£©«у÷§£Ї°чADE°’°чBFE£ї
£®2£©»зЌЉ2£ђµгG «±яBC…ѕ»ќ“в“їµг£®µгG≤ї”лµгB°ҐC÷ЎЇѕ£©£ђЅђљ”AGљїDF”ЏµгH£ђЅђљ”HC£ђєэµгA„чAK°ќHC£ђљїDF”ЏµгK£Ѓ
Ґў«у÷§£ЇHC=2AK£ї
ҐЏµ±µгG «±яBC÷–µг ±£ђ«°”–HD=nHK£®nќ™’э’ы э£©£ђ«уnµƒ÷µ£Ѓ

≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
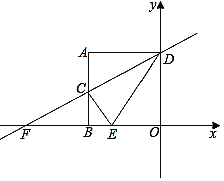
°Њћвƒњ°њ»зЌЉ£ђA(£≠2£ђ2£©°ҐAB°Ќx÷б”ЏµгB£ђAD°Ќy÷б”ЏµгD£ђC£®£≠2£ђ1£©ќ™ABµƒ÷–µг£ђ÷±ѕяCDљїx÷б”ЏµгF£Ѓ
£®1£©«у÷±ѕяCDµƒЇѓ эєЎѕµ љ£ї
£®2£©єэµгC„чCE°ЌDF«“љїx÷б”ЏµгE£ђ«у÷§£Ї°ѕADC£љ°ѕEDC£ї
£®3£©«уµгE„ш±к£ї
£®4£©µгP «÷±ѕяCE…ѕµƒ“їЄцґѓµг£ђ«уPB£ЂPFµƒ„о–°÷µ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com