
����Ŀ��ij���ξ�����������Ʊ������Ʊ����ͯƱ���Ź�Ʊ���Ź�Ʊ�۵��ڳ���Ʊ�����ڶ�ͯƱ����һ���Թ�Ʊ��ﵽһ��������![]() ij��������8����ͯ��������þ���ij���Ʊ�Ͷ�ͯƱ����3040Ԫ�����г���Ʊ�ܷ����Ƕ�ͯƱ�ܷ��õ�
ij��������8����ͯ��������þ���ij���Ʊ�Ͷ�ͯƱ����3040Ԫ�����г���Ʊ�ܷ����Ƕ�ͯƱ�ܷ��õ�![]() �������Ӷ�ͯΪ���ˣ����ٶ���2����Ʊ�����ɴﵽ�����Ź�������Ҫ�������Ű��Ź�Ʊ��Ʊ�ܷ��ÿɽ�Լ40Ԫ��
�������Ӷ�ͯΪ���ˣ����ٶ���2����Ʊ�����ɴﵽ�����Ź�������Ҫ�������Ű��Ź�Ʊ��Ʊ�ܷ��ÿɽ�Լ40Ԫ��
![]() ��þ����ͯ��Ʊ�ĵ��ۣ�
��þ����ͯ��Ʊ�ĵ��ۣ�
![]() ��5�ų���Ʊ������6���Ź�Ʊ������ͬ������������ŵ��������þ��������Ʊ�ĵ��ۣ�
��5�ų���Ʊ������6���Ź�Ʊ������ͬ������������ŵ��������þ��������Ʊ�ĵ��ۣ�
���𰸡���1���þ����ͯ��Ʊ�ĵ���Ϊÿ��80Ԫ����2����������ŵ�������Ϊ28�ˣ��þ��������Ʊ�ĵ���120Ԫ��
��������
![]() ��þ����ͯ��Ʊ�ĵ���ΪxԪ����8����ͯ�ܵ���Ʊ��Ϊ8xԪ��������Ʊ���ܷ���Ϊ
��þ����ͯ��Ʊ�ĵ���ΪxԪ����8����ͯ�ܵ���Ʊ��Ϊ8xԪ��������Ʊ���ܷ���Ϊ![]() Ԫ���ݴ��г����̣���⼴�ɣ�
Ԫ���ݴ��г����̣���⼴�ɣ�
![]() ��������ų�������Ϊy�ˣ�ÿһ���Ź�Ʊ�ĵ���ΪzԪ����
��������ų�������Ϊy�ˣ�ÿһ���Ź�Ʊ�ĵ���ΪzԪ����![]() ֪��������Ʊ�۷�Ϊ
֪��������Ʊ�۷�Ϊ![]() Ԫ
Ԫ![]() �������Ʊ��Ϊ
�������Ʊ��Ϊ![]() Ԫ���ݴ��г����̣���⼴��.
Ԫ���ݴ��г����̣���⼴��.
�⣺![]() ��þ����ͯ��Ʊ�ĵ���ΪxԪ����8����ͯ�ܵ���Ʊ��Ϊ8xԪ��������Ʊ���ܷ���Ϊ
��þ����ͯ��Ʊ�ĵ���ΪxԪ����8����ͯ�ܵ���Ʊ��Ϊ8xԪ��������Ʊ���ܷ���Ϊ![]() Ԫ��
Ԫ��
������ɵã�![]() ��
��
��������̣���![]() ��
��
���ԣ��þ����ͯ��Ʊ�ĵ���Ϊÿ��80Ԫ��
![]() ��������ų�������Ϊy�ˣ�ÿһ���Ź�Ʊ�ĵ���ΪzԪ��
��������ų�������Ϊy�ˣ�ÿһ���Ź�Ʊ�ĵ���ΪzԪ��
��![]() ֪��������Ʊ�۷�Ϊ
֪��������Ʊ�۷�Ϊ![]() Ԫ
Ԫ![]() �������Ʊ��Ϊ
�������Ʊ��Ϊ![]() Ԫ��
Ԫ��
�����⣬��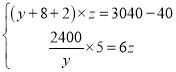 ��
��
����������飬��![]() ��
��
������֪��![]() ��ԭ������Ľ⣬
��ԭ������Ľ⣬
![]() ��������ŵ�������Ϊ
��������ŵ�������Ϊ![]() ��
��![]() ��
��
�þ��������Ʊ�ĵ���Ϊ![]() Ԫ
Ԫ![]() ��
��
����������ŵ�������Ϊ28�ˣ��þ��������Ʊ�ĵ���120Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017��12��3����5�գ����Ľ����绥����������㽭ʡ�������.�����ڼ䣬ij��˾�����˳��У������Ǹ��ܵ������������۴�����ȫ������.С�Ź�����Կ�ۺ�ë�����������Ʒ��15�����뿪���к��յ�������ʾ������Կ��֧��240Ԫ������ë�����֧��180Ԫ.��֪ë����ߵĵ�����Կ�۵��۵�1.5������ôԿ�ۺ�ë����ߵĵ��۸��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ����AB��2������AM��BNΪ��ԲO������.��AM��ȡһ��D������BD����Բ�ڵ�C������AC.��O����BC�Ĵ���OE������Ϊ��E����BN�ཻ�ڵ�F.��D������ԲO������DP���е�ΪP����BN�ཻ�ڵ�Q.
��1������ABD�ա�BFO����BQ�ij���
��2����֤��FQ=BQ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
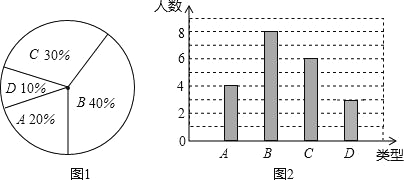
����Ŀ��ijУ260��ѧ���μ�ֲ���,Ҫ��ÿ��ֲ4~7��,���������������������ѧ��ÿ�˵�ֲ����,����Ϊ��������, A��4�ã�B��5�ã�C��6�ã�D:7��,��������������Ƴ�����ͼ(��ͼ1)������ͼ(��ͼ2),��ش���������:
(1)����ε�����D�����ж�����ѧ��?
(2)д��������ѧ��ÿ��ֲ��������������λ����
(3)����ѧ��ÿ��ֲ������ƽ����,��������260��ѧ����ֲ�����ٿã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��ֱ����A��m��0����B��m��2��0������ֱ��x���ֱ��l1��l2��̽��ֱ�� l1��l2�뺯��y=![]() ��ͼ��˫���ߣ�֮��Ĺ�ϵ�����н��۴������( )
��ͼ��˫���ߣ�֮��Ĺ�ϵ�����н��۴������( )
A.����ֱ��������һ����˫�����ཻ
B.�� m��1 ʱ������ֱ����˫���ߵĽ��㵽ԭ��ľ������
C.�� m��0 ʱ������ֱ����˫���ߵĽ��㶼�� y �����
D.�� m��0 ʱ������ֱ����˫���ߵĽ��㶼�� y ���Ҳ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
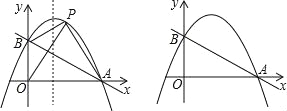
����Ŀ����ͼ��ֱ��y=��![]() x+1��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=��x2+bx+c����A��B���㣮
x+1��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=��x2+bx+c����A��B���㣮
��1���������ߵĽ���ʽ��
��2����P�ǵ�һ�����������ϵ�һ�㣬����PA��PB��PO������POA���������POB�����![]() ����
����
�����P�����ꣻ
����QΪ�����߶Գ�����һ�㣬��ֱ��д��QP+QA����Сֵ��
��3����MΪֱ��AB�ϵĶ��㣬��NΪ�������ϵĶ��㣬���Ե�O��B��M��NΪ������ı�����ƽ���ı���ʱ����ֱ��д����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���Rt��ABC�У���BAC=90�㣬D��AC���е㣬CE��BD�ڵ�E����BA���ӳ����ڵ�F����BF=12�����FBC�����Ϊ( )

A. 40 B. 46 C. 48 D. 50
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������������У���ABCΪ��������Σ��������εĶ��㶼�ڸ���ϣ���

��1������ABC��BA����ƽ�ƺ�A�Ƶ���A1���������л���ƽ�ƺ�õ�����A1B1C1��
��2������A1B1C1�Ƶ�A1����ʱ�뷽����ת90�����������л�����ת�����A1B2C2��
��3�����������С�����εı߳�Ϊ1�����B������1������2���任��·���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2+��k+3��x+![]() =0����������ȵ�ʵ������
=0����������ȵ�ʵ������
��1����k��ȡֵ��Χ��
��2������������Ϊx1��x2����ô�Ƿ����ʵ��k��ʹ�õ�ʽ![]() =��1�����������ڣ����k��ֵ���������ڣ���˵�����ɣ�
=��1�����������ڣ����k��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com