
【题目】已知关于x的方程x2+(k+3)x+![]() =0有两个不相等的实数根.
=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若方程两根为x1,x2,那么是否存在实数k,使得等式![]() =﹣1成立?若存在,求出k的值;若不存在,请说明理由.
=﹣1成立?若存在,求出k的值;若不存在,请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某旅游景点有三种门票:成人票、儿童票和团购票,团购票价低于成人票、高于儿童票,但一次性购票需达到一定的数量![]() 某旅游团有8名儿童,若购买该景点的成人票和儿童票共需3040元,其中成人票总费用是儿童票总费用的
某旅游团有8名儿童,若购买该景点的成人票和儿童票共需3040元,其中成人票总费用是儿童票总费用的![]() 倍;若视儿童为成人,并再多买2张门票,即可达到景点团购的数量要求,旅游团按团购票购票总费用可节约40元.
倍;若视儿童为成人,并再多买2张门票,即可达到景点团购的数量要求,旅游团按团购票购票总费用可节约40元.
![]() 求该景点儿童门票的单价;
求该景点儿童门票的单价;
![]() 若5张成人票费用与6张团购票费用相同,求这个旅游团的总人数和该景点成人门票的单价?
若5张成人票费用与6张团购票费用相同,求这个旅游团的总人数和该景点成人门票的单价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°.

(1)求∠DOE的度数;
(2)OF平分∠AOD吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
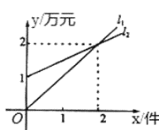
【题目】如图,![]() 表示某机床公司一天的销售收入与机床销售量的关系,
表示某机床公司一天的销售收入与机床销售量的关系,![]() 表示该公司一天的销售成本与机床销售量的关系.有以下四个结论:①
表示该公司一天的销售成本与机床销售量的关系.有以下四个结论:①![]() 对应的函数表达式是y=x;②
对应的函数表达式是y=x;②![]() 对应的函数表达式是y=x+1;③当销售量为2件时,销售收入等于销售成本;④利润与销售量之间的函数表达式是w=0.5x-1.其中正确的结论为____(请把所有正确的序号填写在横线上).
对应的函数表达式是y=x+1;③当销售量为2件时,销售收入等于销售成本;④利润与销售量之间的函数表达式是w=0.5x-1.其中正确的结论为____(请把所有正确的序号填写在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
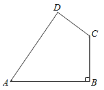
(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为表彰在“创文明城,点赞泰城”书画比赛中表现优秀的同学,决定购买水彩盒或钢笔作为奖品。已知1个水彩盒28元、1支钢笔30元。
(1)恰逢“十一”商店举行“优惠促销”活动,具体办法如下:水彩盒“九折”优惠;钢笔10支以上超出部分“八折”优惠。若买![]() 个水彩盒需要
个水彩盒需要![]() 元,买
元,买![]() 支钢笔需要
支钢笔需要![]() 元,求
元,求![]() ,
,![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(2)当购买数量为多少时,购买两种奖品的费用相同?
(3)当购买数量为80时,购买两种奖品的费用差距是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若 ![]() 为数轴上三点,若点
为数轴上三点,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 的距离
的距离![]() 倍,我们就称点
倍,我们就称点![]() 是
是![]() 的巧点.若
的巧点.若 ![]() 为数轴上三点,若点
为数轴上三点,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到 ![]() 的距离一半,我们就称点
的距离一半,我们就称点![]() 是
是![]() 的妙点.如图,点
的妙点.如图,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,表示
,表示![]() 的点
的点![]() 到点
到点![]() 的距离是
的距离是![]() ,到点
,到点![]() 的距离是
的距离是![]() ,那么点
,那么点![]() 是
是![]() 的巧点,点
的巧点,点![]() 是
是![]() 的妙点.
的妙点.
![]()
知识运用:
(1)如图 1,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,那么点
,那么点![]() 是(
是(![]() 的( )
的( )
![]()
A.巧点 B. 妙点 C. 无法确定
(2)如图 2,![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为
所表示的数为![]() ,则(
,则(![]() 的巧点表示的数是 ;
的巧点表示的数是 ;
![]()

拓展提升
(3)如图 3,![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为
所表示的数为![]() .现有一只电子蚂蚁P从点
.现有一只电子蚂蚁P从点 ![]() 出发,以每
出发,以每![]() 秒单位的速度向右运动,到达点
秒单位的速度向右运动,到达点![]() 停止. 当经过几秒时,
停止. 当经过几秒时,![]() 和
和 ![]() 其有一个点为其余两点的巧点? (请直接写出结果)
其有一个点为其余两点的巧点? (请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市需调查该市九年级男生的体能状况,为此抽取了50名九年级男生进行引体向上个数测试,测试情况绘制成表格如下:
个数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
人数 | 1 | 1 | 6 | 18 | 10 | 6 | 2 | 2 | 1 | 1 | 2 |
(1)求这次抽样测试数据的平均数、众数和中位数;
(2)在平均数、众数和中位数中,你认为用哪一个统计量作为该市九年级男生引体向上项目测试的合格标准个数较为合适?简要说明理由;
(3)如果该市今年有3万名九年级男生,根据(2)中你认为合格的标准,试估计该市九年级男生引体向上项目测试的合格人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
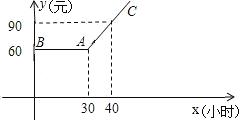
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com