
【题目】如图,AB为一斜坡,其坡角为19.5°,紧挨着斜坡AB底部A处有一高楼,一数学活动小组量得斜坡长AB=15m,在坡顶B处测得楼顶D处的仰角为45°,其中测量员小刚的身高BC=1.7米,求楼高AD.
(参考数据:sin19.5°≈ ![]() ,tan19.5°≈
,tan19.5°≈ ![]() ,最终结果精确到0.1m).
,最终结果精确到0.1m).
【答案】解:作CF⊥AD于点F.
在Rt△ABE中,∵AB=15,
∴BE=ABsin19.5°=15sin19.5°,
AE=ABcos19.5°=15cos19.5°,
在Rt△CDF中,∵CF=AE,∠DCF=45°,
∴DF=CF,
∴AD=DF+AF=CF+BC+BE=15cos19.5°+1.7+15sin19.5°≈21.0(m).
答:楼高AD为21.0米.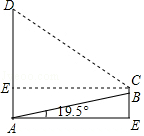
【解析】作CF⊥AD于点F,在直角△ABE中求得BE,和AE的长,然后在直角△CDE中利用三角函数求得DE的长,根据AD=DF+AF=CF+BC+BE求解.
【考点精析】根据题目的已知条件,利用关于坡度坡角问题的相关知识可以得到问题的答案,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图示,三角形ABC是等边三角形,D是BC边上的一点,三角形ABD经过旋转后到达三角形ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M到了什么位置?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是( ) 
A.![]()
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )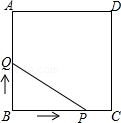
A.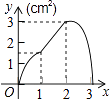
B.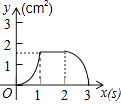
C.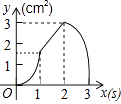
D.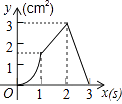
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E. 
(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,“回”字形的道路宽为1米,整个“回”字形的长为8米,宽为1米,一个人从入口点A沿着道路中央走到中点B,他共走了( )

A. 55米 B. 55.5米 C. 56米 D. 56.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有点a,b,c三点
![]()
(1)用“<”将a,b,c连接起来.
(2)b﹣a 1(填“<”“>”,“=”)
(3)化简|c﹣b|﹣|c﹣a+1|+|a﹣1|
(4)用含a,b的式子表示下列的最小值:
①|x﹣a|+|x﹣b|的最小值为 ;
②|x﹣a|+|x﹣b|+|x+1|的最小值为 ;
③|x﹣a|+|x﹣b|+|x﹣c|的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com