
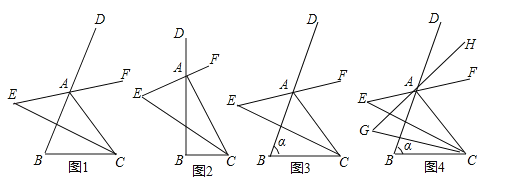
【题目】如图,在△ABC中,分别作其内角∠ACB与外角∠DAC的角平分线,且两条角平分线所在的直线交于点E
(1)填空:①如图1,若∠B=60°,则∠E= ;
②如图2,若∠B=90°,则∠E= ;
(2)如图3,若∠B=α,求∠E的度数;
(3)如图4,仿照(2)中的方法,在(2)的条件下分别作∠EAB与∠ECB的角平分线,且两条角平分线交于点G,求∠G的度数.
【答案】(1)①30°;②45°;(2)∠E=![]() α;(3)∠G =
α;(3)∠G =![]() α.
α.
【解析】
(1)①根据三角形的外角性质可得∠DAC﹣∠ACB=∠B=60°,再根据角平分线的定义可得∠FAC﹣∠ACE=30°,可求∠E的度数;
②根据三角形的外角性质可得∠DAC﹣∠ACB=∠B=90°,再根据角平分线的定义可得∠FAC﹣∠ACE=45°,可求∠E的度数;
(2)根据三角形的外角性质可得∠DAC﹣∠ACB=∠B=![]() α,再根据角平分线的定义可得∠FAC﹣∠ACE=
α,再根据角平分线的定义可得∠FAC﹣∠ACE=![]() α,可求∠E的度数;
α,可求∠E的度数;
(3)根据角平分线的定和义可得三角形的外角性质可得∠G=∠HAC﹣∠ACG=![]() ∠FAC﹣
∠FAC﹣![]() ∠ACE=
∠ACE=![]() (∠FAC﹣∠ACE),可求∠G的度数.
(∠FAC﹣∠ACE),可求∠G的度数.
(1)①∠DAC﹣∠ACB=∠B=60°.
∵EA平分∠DAC,EC平分∠ACB,∴∠FAC=![]() ∠DAC,∠ACE=
∠DAC,∠ACE=![]() ∠ACB,∴∠E=∠FAC﹣∠ACE=
∠ACB,∴∠E=∠FAC﹣∠ACE=![]() ∠B=30°;
∠B=30°;
②∠DAC﹣∠ACB=∠B=60°.
∵EA平分∠DAC,EC平分∠ACB,∴∠FAC=![]() ∠DAC,∠ACE=
∠DAC,∠ACE=![]() ∠ACB,∴∠E=∠FAC﹣∠ACE=
∠ACB,∴∠E=∠FAC﹣∠ACE=![]() ∠B=45°;
∠B=45°;
(2)∠DAC﹣∠ACB=∠B=α.
∵EA平分∠DAC,EC平分∠ACB,∴∠FAC=![]() ∠DAC,∠ACE=
∠DAC,∠ACE=![]() ∠ACB,∴∠E=∠FAC﹣∠ACE=
∠ACB,∴∠E=∠FAC﹣∠ACE=![]() ∠B=
∠B=![]() α;
α;
(3)∵AG,CG分别是∠EAB与∠ECB的角平分线,∴∠G=∠HAC﹣∠ACG=![]() ∠FAC﹣
∠FAC﹣![]() ∠ACE=
∠ACE=![]() (∠FAC﹣∠ACE)=
(∠FAC﹣∠ACE)=![]() ×
×![]() ∠B=
∠B=![]() α.
α.


科目:初中数学 来源: 题型:
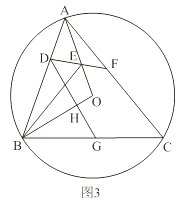
【题目】有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形ABCD中,∠B=![]() ∠D,∠C=
∠D,∠C=![]() ∠A,求∠B与∠C的度数之和;
∠A,求∠B与∠C的度数之和;

(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO.∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.

求证:四边形DBCF是半对角四边形;
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G.当DH=BG时,求△BGH与△ABC的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
对于二次三项式![]() 可以直接用公式法分解为
可以直接用公式法分解为![]() 的形式,但对于二次三项式
的形式,但对于二次三项式![]() ,就不能直接用公式法了,我们可以在二次三项式
,就不能直接用公式法了,我们可以在二次三项式![]() 中先加上一项
中先加上一项![]() ,使其成为完全平方式,再减去
,使其成为完全平方式,再减去![]() 这项,使整个式子的值不变.于是有
这项,使整个式子的值不变.于是有![]() =
=![]() +
+![]() -
-![]() =
=![]() =
=![]() .
.
像上面这样把二次三项式分解因式的方法叫做添(拆)项法.
(1)请用上述方法把x2-4x+3分解因式.
(2)多项式x2+2x+2有最小值吗?如果有,那么当它有最小值时x的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=100°,∠BCD=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的盒子里装有30个除颜色外其它均相同的球,其中红球有m个,白球有3m个,其它均为黄球.现小李从盒子里随机摸出一个球,若是红球,则小李获胜;小李把摸出的球放回盒子里摇匀,由小马随机摸出一个球,若为黄球,则小马获胜.
(1)当m=4时,求小李摸到红球的概率是多少?
(2)当m为何值时,游戏对双方是公平的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在小学已经学过了“对边分别平行的四边形叫做平行四边形”,如图1,平行四边形MNPQ的一边PQ作左右平移,图2反映它的边NP的长度(cm)随时间t(s)变化而变化的情况,请解答下列问题:
(1)在这个变化过程中,自变量是______,因变量是______;
(2)观察图2,PQ向左平移前,边NP的长度是______cm,请你根据图象呈现的规律写出0至5秒间l与t的关系式;
(3)填写下表,并根据表中呈现的规律写出8至14秒间1与t的关系式.
PQ边的运动时间/s | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
NP的长度/cm | 18 | 15 | 12 | ______ | 6 | 3 | 0 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADC都是边长相等的等边三角形,点E、F同时分别从点B、A出发,各自沿BA、AD方向运动到点A、D停止,运动的速度相同,连接EC、FC.
(1)在点E、F运动过程中∠ECF的大小是否随之变化?请说明理由;
(2)在点E、F运动过程中,以点A、E、C、F为顶点的四边形的面积变化了吗?请说明理由;
(3)连接EF,在图中找出和∠ACE相等的所有角,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空:把下面的推理过程补充完整,并在括号内注明理由,
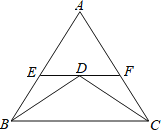
如图,已知△ABC中,E、F分别是AB、AC上的两点,且EF∥BC,D为EF上一点,且BD=CD,ED=FD,请说明BE=CF.
解:∵BD=CD(已知)
∴∠DBC=∠DCB(______)
∵EF∥BC(已知)
∴∠EDB=∠DBC
∠FDC=______(______)
∴∠EDB=∠FDC(等量代换)
在△EBD和△FCD中,
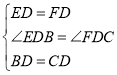
∴△EBD≌△FCD(______)
∴BE=CF(______)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com