
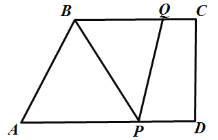
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() ,动点P从点D出发,沿射线
,动点P从点D出发,沿射线![]() 的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段
的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段![]() 上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)
上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)
(1)设![]() 的面积为S,求S与t之间的函数关系式;
的面积为S,求S与t之间的函数关系式;
(2)若四边形![]() 为平行四边形,求运动时间t;
为平行四边形,求运动时间t;
(3)当t为何值时,以B、P、Q三点为顶点的三角形是等腰三角形?
【答案】(1) ![]() ; (2)
; (2) ![]() ; (3)
; (3) ![]() 或者t=3.6
或者t=3.6
【解析】
(1) 根据![]() 可得
可得![]() ,再根据三角形面积的求法,求出S与t之间的函数关系式即可;
,再根据三角形面积的求法,求出S与t之间的函数关系式即可;
(2)根据平行四边形的判定定理得到AP=BQ时四边形ABQP是平行四边形,再求出t即可得到答案;
(3)根据题意分三种情况(PB=PQ,PQ=BQ,PB=BQ),再根据等腰三角形的性质,分类讨论求出t即可得到答案;
解:(1) ∵BC=20,动点Q以每秒1个单位长的速度向点B运动,点P从点D出发,沿射线![]() 的方向以每秒2个单位长的速度运动,
的方向以每秒2个单位长的速度运动,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴CD的长度是![]() 以BQ为底边的高的长度,
以BQ为底边的高的长度,
∴![]() ;
;
(2)如下图:

由题意得:![]() ,
,![]() ,
,
∵![]() ,
,
∴当AP=BQ时,四边形ABQP是平行四边形(一组对边平行且相等的四边形是平行四边形),
即:![]() ,
,
解得:![]() ;
;
(3)情况1:如下图:作PN⊥BC与点N,

当PB=PQ时,
NQ=BN(三线合一定理),
∵NQ=PD-CQ=2t-t=t,
∴BN=t,BQ=2t,
∵BC-BQ=CQ
∴20-2t=t,
解得:![]() ;
;
情况2:如图,作PN⊥BC与点N,

当PQ=BQ时,
NQ=PD-CQ=2t-t=t,
PQ=BQ=20-t,
在直角三角形NPQ中,
![]() (勾股定理),
(勾股定理),
∴![]() ,
,
解得t=3.6;
情况3:如图,

当PB=BQ时,
BN=20-2t,
BP=BQ=20-t,
在直角三角形BNP中,
![]() (勾股定理),
(勾股定理),
∴![]() ,
,
整理得:![]()
![]() ,
,
故方程无解,综上可得:![]() 或者t=3.6时,以B、P、Q三点为顶点的三角形是等腰三角形.
或者t=3.6时,以B、P、Q三点为顶点的三角形是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.

(1)求抛物线的解析式;
(2)在直线BC上找点D,使△ABD为以AB为腰的等腰三角形,求D点的坐标;
(3)在抛物线上是否存在异于B的点P,过P点作PQ⊥AC于Q,使△APQ与△ABC相似?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E是边BC的中点,DE的延长线与AB的延长线相交于点F.
(1)求证:△CDE≌△BFE;
(2)试连接BD、CF,判断四边形CDBF的形状,并证明你的结论

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
如图,∠C=50°,E是BA延长线上的一点,过点A作![]() //BC﹒若AD平分∠CAE,求∠B的度数.
//BC﹒若AD平分∠CAE,求∠B的度数.

解:∵![]() //BC,∠C=50°( 已知 ),
//BC,∠C=50°( 已知 ),
∴∠2= = °( ).
又∵AD平分∠CAE( 已知 ),
∴ =∠2=50°( ).
又∵![]() //BC(已知),
//BC(已知),
∴∠B= = °( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了迎接体育中考,3月底对初三某班学生进行了一次跳绳测试,测试成绩分别记为A,B,C,D,E共5个等级(其中D,E为优良),并绘制成了统计图1.在进行了为期一个月的特训后,4月底对同一批学生又进行了一次跳绳测试,发现A类的人数没有发生变化,并将成绩绘制成统计图2.请根据图中提供的信息,解答下列问题:
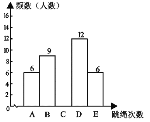

图1 图2
(1)求此次参加测试的学生人数;
(2)补全频数分布直方图和扇形统计图C为____;
(3)请估计该校九年级500名学生在进行一个月的特训后,优良人数增加了多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(8,0),点B为y轴负半轴上的一动点,分别以OB,AB为直角边在第三、第四象限作等腰直角三角形OBF,等腰直角三角形ABE,连接EF交y轴与P点,当点B在y轴上移动时,则PB的长度是( )
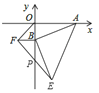
A.2B.4C.不是已知数的定值D.PB的长度随点B的运动而变化
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()
A.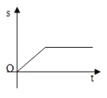 B.
B.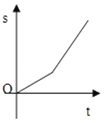 C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com