
【题目】如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度? 
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D. 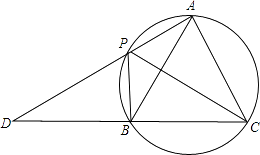
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=2 ![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是 . (写出正确命题的序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在海上观察所A,我边防海警发现正北5km的B处有一可疑船只正在向东方向12km的C处行驶.我边防海警即刻派船前往C处拦截.若可疑船只的行驶速度为60km/h,则我边防海警船的速度为多少时,才能恰好在C处将可疑船只截住?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(﹣1,m)和点B(n,5). 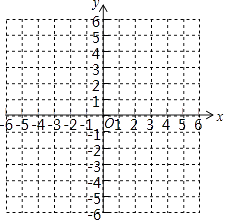
(1)求该二次函数的关系式;
(2)在给定的平面直角坐标系中,画出这两个函数的大致图象;
(3)结合图象直接写出x2+bx+c>x+1时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com