
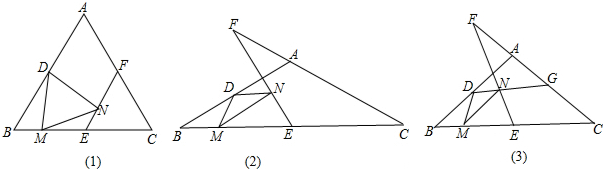
分析 (1)连接DE,先证明BD=BE=DE,再由SAS证明△BDE△BDM≌△EDN,得出∠DEF=∠B=60°,证明△EFC是等边三角形,得出CF=CE,即可得出结论;
(2)连接DE,作EH⊥CF于H,由等腰三角形的性质得出∠B=∠C=30°,同(1)得:△BDM≌△EDN,得出∠DEN=∠B=30°,NE=BM,证出EF=CE,得出CH=FH=$\frac{1}{2}$CF,由含30°角的直角三角形的性质得出CH=$\frac{\sqrt{3}}{2}$CE,CF=$\sqrt{3}$CE,即可得出结论;
(3)连接AE、DE,由等腰三角形的性质得出AE⊥BC,由含30°角的直角三角形的性质得出AE=$\frac{1}{2}$AB=$\frac{3\sqrt{3}}{2}$,得出BE=$\sqrt{3}$AE=$\frac{9}{2}$,求出EF=BE=$\frac{9}{2}$,得出FN=EF-NE=$\frac{5}{2}$,作MK⊥AB于K,得出BK=$\sqrt{3}$MK=$\sqrt{3}$,DK=BD-BK=$\frac{\sqrt{3}}{2}$,由勾股定理求出DN=DM=$\sqrt{M{K}^{2}+D{K}^{2}}$=$\frac{\sqrt{7}}{2}$,再由平行线得出比例式求出NG,即可DG的长.
解答 (1)证明:连接DE,如图1所示
∵点D,E分别为边AB,BC的中点,
∴DE是△ABC的中位线,BD=$\frac{1}{2}$AB,BE=CE=$\frac{1}{2}$BC,
∴DE∥AC,DE=$\frac{1}{2}$AC,
∵∠A=60°,AB=AC,
∴△ABC是等边三角形,
∴AB=AC=BC,∠B=∠C=60°,
∴BD=BE=DE,即△BDE是等边三角形,
∴∠BED=∠BDE=60°,
∵∠MDN=∠A=60°,
∴∠BDM=∠EDN,
在△BDM和△EDN中,$\left\{\begin{array}{l}{BD=ED}&{\;}\\{∠BDM=∠EDN}&{\;}\\{DM=DN}&{\;}\end{array}\right.$,
∴△BDM≌△EDN(SAS),
∴∠DEF=∠B=60°,
∴∠FEC=60°,
∴∠EFC=180°-60°-60°=60°,
∴△EFC是等边三角形,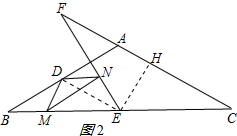
∴CF=CE,
∴CF=BE;
(2)CF=$\sqrt{3}$BE;理由如下:连接DE,作EH⊥CF于H,如图2所示:
∵∠A=120°,AB=AC,
∴∠B=∠C=30°,
由(1)得:DE=$\frac{1}{2}$AC,BD=$\frac{1}{2}$AB,
∴BD=DE,
∴∠DEB=∠B=30°,
同(1)得:△BDM≌△EDN,
∴∠DEN=∠B=30°,NE=BM,
∴∠BEF=60°,
又∵∠BEF=∠C+∠F,
∴∠F=30°=∠C,
∴EF=CE,∴CH=FH=$\frac{1}{2}$CF,
∵∠C=30°,
∴CH=$\frac{\sqrt{3}}{2}$CE,
∴CF=$\sqrt{3}$CE,
∵BE=CE,
∴CF=$\sqrt{3}$BE;
故答案为:CF=$\sqrt{3}$BE;
(3)解:连接AE、DE,如图3所示:
∵AB=AC,E是BC的中点,
∴AE⊥BC,
∵∠B=30°,
∴AE=$\frac{1}{2}$AB=$\frac{3\sqrt{3}}{2}$,
∴BE=$\sqrt{3}$AE=$\frac{9}{2}$,
∴EF=BE=$\frac{9}{2}$,
∴FN=EF-NE=$\frac{5}{2}$,
作MK⊥AB于K,
∵∠B=30°,
∴MK=$\frac{1}{2}$BM=1,
∴BK=$\sqrt{3}$MK=$\sqrt{3}$,
∵BD=$\frac{1}{2}$AB=$\frac{3\sqrt{3}}{2}$,
∴DK=BD-BK=$\frac{\sqrt{3}}{2}$,
∴DN=DM=$\sqrt{M{K}^{2}+D{K}^{2}}$=$\frac{\sqrt{7}}{2}$,
∵DE∥AC,
∴$\frac{DN}{NG}=\frac{NE}{FN}$,
即$\frac{\frac{\sqrt{7}}{2}}{NG}=\frac{2}{\frac{5}{2}}$,
解得:NG=$\frac{5\sqrt{7}}{8}$,
∴DG=DN+NG=$\frac{\sqrt{7}}{2}$+$\frac{5\sqrt{7}}{8}$=$\frac{9\sqrt{7}}{8}$.
点评 本题是相似形综合题目,考查了等边三角形的性质与判定、全等三角形的判定与性质、等腰三角形的性质、三角形中位线定理、勾股定理、含30°角的直角三角形的性质、平行线分线段成比例定理等知识;本题综合性强,难度较大,需要通过作辅助线证明三角形全等和运用勾股定理等知识才能得出结果.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
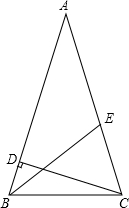 如图,在△ABC中,AB=AC,CD⊥AB,CE=2BD.
如图,在△ABC中,AB=AC,CD⊥AB,CE=2BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8cm,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值是8cm.
如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8cm,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值是8cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com