
 如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8cm,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值是8cm.
如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8cm,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值是8cm. 分析 设点P关于OA的对称点为C,关于OB的对称点为D,当点M、N在CD上时,△PMN的周长最小.
解答 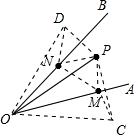 解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.
解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM=CM,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PN=DN,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=8cm,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=OD=8cm.
∴△PMN的周长的最小值=PM+MN+PN=CM+MN+DN≥CD=8cm.
故答案为:8cm.
点评 此题主要考查轴对称--最短路线问题,熟知两点之间线段最短是解答此题的关键.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
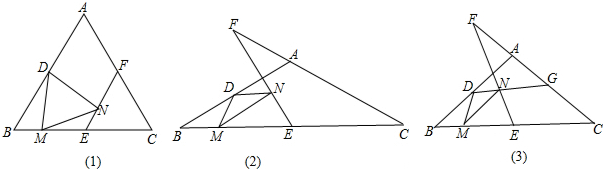
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
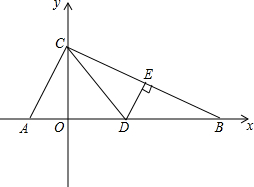 如图,在平面直角坐标系内,已知A(-4,0),B(16,0),点C在y轴正半轴上,且∠ACB=90°,D,E分别为线段AB,BC上的点,把△BDE沿直线DE翻折,使点B落在点C处.
如图,在平面直角坐标系内,已知A(-4,0),B(16,0),点C在y轴正半轴上,且∠ACB=90°,D,E分别为线段AB,BC上的点,把△BDE沿直线DE翻折,使点B落在点C处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y=x2+bx+4与x轴交于点B(4,0),与y轴交于点A,O为坐标原点,P是二次函数y=x2+bx+4的图象上一个动点,点P的横坐标是m,且m>4,过点P作PM⊥x轴,PM交直线AB于M.
如图,已知二次函数y=x2+bx+4与x轴交于点B(4,0),与y轴交于点A,O为坐标原点,P是二次函数y=x2+bx+4的图象上一个动点,点P的横坐标是m,且m>4,过点P作PM⊥x轴,PM交直线AB于M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com