【题目】如图：在平行四边形ABCD中，点E在BA的延长线上，且BE=AD，点F在AD上，AF=AB，求证：CF=EF．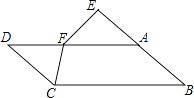 
【答案】证明：∵四边形ABCD是平行四边形，
∴CD∥AB，CD=AB，
∴∠D=∠EAF，
∵BE=AD，AF=AB，
∴AE=DF，CD=AF，
在△CDF和△FAE中，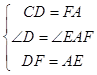
，
∴△DCF≌△AFE（SAS），
∴CF=EF．
【解析】由四边形ABCD是平行四边形，可得CD∥AB，CD=AB，即可证得∠D=∠EAF，又由BE=AD，AF=AB，易得AE=DF，CD=AF，然后由SAS证得△DCF≌△AFE，即可证得结论．
【考点精析】本题主要考查了平行四边形的性质的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能正确解答此题．
科目：初中数学 来源： 题型：
【题目】如图，在等边三角形ABC中，AB=6，点P是AB边上的任意一点（点P不与点A、点B重合），过点P作PD⊥AB，交直线BC于点D，作PE⊥AC，垂足为点F．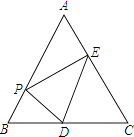 
（1）求∠APE的度数；
（2）连接DE，当△PDE为等边三角形时，求BP的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市最高气温是33℃，最低气温是24℃，则该市气温t（℃）的变化范围是（）
A. t＞33 B. t≤24 C. 24＜t＜33 D. 24≤t≤33
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在平面直角坐标系中，有矩形AOBC，点A、B的坐标分别为（0，4）、（10,0），点P的坐标为（2，0），点M在线段AO上，点N在线段AC上，总有∠MPN=90 ，点M从点O运动到点A，当点M运动到A点时，点N与点C重合（如图2）。令AM=x
（1）.直接写出点C的坐标___________；
（2）、①设MN2=y，请写出y关于x的函数关系式，并求出y的最小值；
②连接AP交MN于点D，若MN⊥A P，求x的值；
（3）、当点M在边AO上运动时，∠PMN的大小是否发生变化？请说明理由.
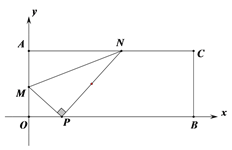
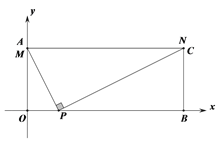
图1 图2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，一次函数y=ax+b（a≠0）的图形与反比例函数y=
（k≠0）的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=3，tan∠AOH=
，点B的坐标为（m，﹣2）．
（1）求△AHO的周长；
（2）求该反比例函数和一次函数的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列调查中，哪些适合抽样调查？哪些适合全面调查？
(1)工厂准备对一批即将出厂的饮料中含有细菌总数的情况进行调查；
(2)小明准备对全班同学所喜爱的球类运动的情况进行调查；
(3)某农田保护区对区内的水稻秧苗的高度进行调查．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com