
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,把
,把![]() 绕着它的斜边中点
绕着它的斜边中点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() 的位置,
的位置,![]() 交
交![]() 于点
于点![]() .
.![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]()
![]() .
.

A. 8 B. 9 C. 10 D. 12
【答案】B
【解析】
如图,由点P为斜边BC的中点得到PC=![]() BC=6,再根据旋转的性质得PF=PC=6,∠FPC=90°,∠F=∠C=30°,根据含30度的直角三角形三边的关系,在Rt△PFH中计算出PH=
BC=6,再根据旋转的性质得PF=PC=6,∠FPC=90°,∠F=∠C=30°,根据含30度的直角三角形三边的关系,在Rt△PFH中计算出PH=![]() PF=2
PF=2![]() ;在Rt△CPM中计算出PM=
;在Rt△CPM中计算出PM=![]() PC=2
PC=2![]() ,且∠PMC=60°,则∠FMN=∠PMC=60°,于是有∠FNM=90°,FM=PF-PM=6-2
,且∠PMC=60°,则∠FMN=∠PMC=60°,于是有∠FNM=90°,FM=PF-PM=6-2![]() ,则在Rt△FMN中可计算出MN=
,则在Rt△FMN中可计算出MN=![]() FM=3-
FM=3-![]() ,FN=
,FN=![]() MN=3
MN=3![]() -3,然后根据三角形面积公式和利用△ABC与△DEF重叠部分的面积=S△FPH-S△FMN进行计算即可.
-3,然后根据三角形面积公式和利用△ABC与△DEF重叠部分的面积=S△FPH-S△FMN进行计算即可.
如图,
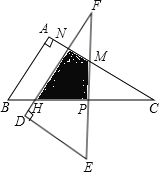
∵点P为斜边BC的中点,
∴PB=PC=![]() BC=6,
BC=6,
∵△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,
∴PF=PC=6,∠FPC=90°,∠F=∠C=30°,
在Rt△PFH中,∵∠F=30°,
∴PH=![]() PF=
PF=![]() ×6=2
×6=2![]() ,
,
在Rt△CPM中,∵∠C=30°,
∴PM=![]() PC=
PC=![]() ×6=2
×6=2![]() ,∠PMC=60°,
,∠PMC=60°,
∴∠FMN=∠PMC=60°,
∴∠FNM=90°,
而FM=PF-PM=6-2![]() ,
,
在Rt△FMN中,∵∠F=30°,
∴MN=![]() FM=3-
FM=3-![]() ,
,
∴FN=![]() MN=3
MN=3![]() -3,
-3,
∴△ABC与△DEF重叠部分的面积=S△FPH-S△FMN
=![]() ×6×2
×6×2![]() -
-![]() (3-
(3-![]() )(3
)(3![]() -3)
-3)
=9(cm2).
故选B.


 培优口算题卡系列答案
培优口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的边AB在x轴上,点B坐标(﹣3,0),点C在y轴正半轴上,且sin∠CBO=![]() ,点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.
,点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.
(1)求点D坐标.
(2)求S关于t的函数关系式.
(3)在直线l移动过程中,l上是否存在一点Q,使以B、C、Q为顶点的三角形是等腰直角三角形?若存在,直接写出Q点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=![]() 的图象交于A,B两点,则四边形MAOB的面积为____________.
的图象交于A,B两点,则四边形MAOB的面积为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)该班共有_____名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为_____;
(4)学校将举办体育节,该班将推选5位同学参加乒乓球活动,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=90°,AD∥BC,以B为圆心,BC长为半径画弧,与射线AD相交于点E,连接BE,过点C作CF⊥BE,垂足为F.若AB=6,BC=10,则EF的长为___________.
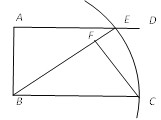
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() 与直线
与直线![]() 交于A、B,直线AB交于y轴于点C,点P为线段OB上一个动点(不与点O、B重合),当△OPC为等腰三角形时,点P的坐标:_______.
交于A、B,直线AB交于y轴于点C,点P为线段OB上一个动点(不与点O、B重合),当△OPC为等腰三角形时,点P的坐标:_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个完全相同的小正方体堆成一个几何体.
![]() 请画出这个几何体的三视图;
请画出这个几何体的三视图;

![]() 现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,那么在这个几何体上最多可以再添加________个小正方体.
现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,那么在这个几何体上最多可以再添加________个小正方体.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com