
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植树4﹣7颗,活动结束后随机抽查了20名学生每人的植树数量,并分为四种类型,A:4颗;B:5颗;C:6颗;D:7颗.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
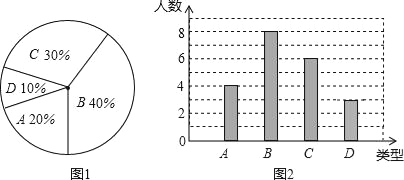
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数和中位数;
(3)求这20名学生每人植树量的平均数,并估计这260名学生共植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB、AC上.
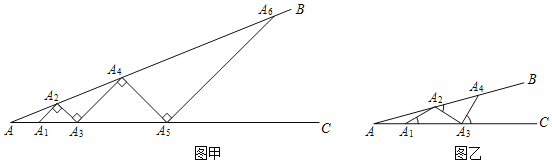
活动一:如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直.(A1A2为第1根小棒)
数学思考:
(1)小棒能无限摆下去吗?答: .(填“能”或“不能”)
(2)设AA1=A1A2=A2A3,求θ的度数;
活动二:如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第一根小棒,且A1A2=AA1.
数学思考:
(3)若已经摆放了3根小棒,则θ1= ,θ2= ,θ3= ;(用含θ的式子表示)
(4)若只能摆放5根小棒,求θ的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB>∠ABC,三条内角平分线AD,BE,CF相交于点I.

(1)若∠ABE=25°,求∠DIC的度数;
(2)在(1)的条件下,图中互余的角有多少对?列举出来;
(3)过I点作IH⊥BC,垂足为H,试问∠BID与∠HIC相等吗?为什么?
(4)G是AD延长线上一点,过G点作GP⊥BC,垂足为P,试探究∠G与∠ABC,∠ACB之间的数量关系,直接写出结论,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向经过点A的直线EF作垂线,垂足为E,F.
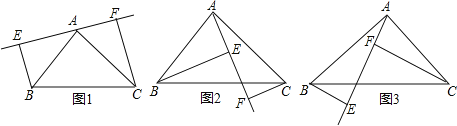
(1)如图1,当EF与斜边BC不相交时,请证明EF=BE+CF;
(2)如图2,当EF与斜边BC相交时,其他条件不变,写出EF、BE、CF之间的数量关系,并说明理由;
(3)如图3,猜想EF、BE、CF之间又存在怎样的数量关系,写出猜想,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点.
AC,E是AC的中点.
(1)求证:BC=DE;
(2)连接AD、BE,若∠BAC=∠C,求证:四边形DBEA是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
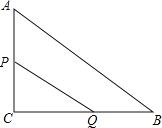
【题目】如图,在![]() 中,
中,![]() 点P、Q同时由A、B两点出发,分别沿AC,BC的方向匀速运动,它们的速度都是每秒1cm,____秒钟后△PCQ的面积等于△ABC的一半?
点P、Q同时由A、B两点出发,分别沿AC,BC的方向匀速运动,它们的速度都是每秒1cm,____秒钟后△PCQ的面积等于△ABC的一半?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.
的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.
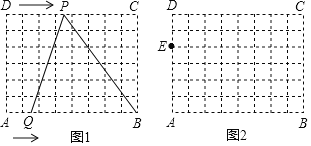
(1)请在![]() 的网格纸图2中画出运动时间t为2秒时的线段PQ并求其长度;
的网格纸图2中画出运动时间t为2秒时的线段PQ并求其长度;
(2)在动点P、Q运动的过程中,△PQB能否成为PQ=BQ的等腰三角形?若能,请求出相应的运动时间t;若不能,请说明理由;
(3)在(1)中的图2中,点E如图所示,是否在PQ上存在一点M,使DM+EM的值最小,如存在,求出DM+EM最小值;如不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将使结论成立的条件或理由填写在横线上或括号内.
如图,![]() 中,
中,![]() 是边
是边![]() 的中点,过点
的中点,过点![]() 作
作![]() , 交
, 交![]() 的延长线于点
的延长线于点![]() .
.
求证:![]() 是
是![]() 的中点.
的中点.

证明:![]()
![]() (已知)
(已知)
![]()
![]()
![]() 是边
是边![]() 的中点
的中点
![]()
在![]() 和
和![]() 中
中

![]()
![]()
![]()
![]() 是
是![]() 的中点.
的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com