
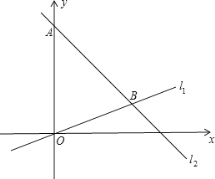
【题目】已知,如图,在平面直角坐标系内,点A的坐标为(0,24 ),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
(1)求直线l1,l2的表达式;
(2)点C为线段OB上一动点 (点C不与点O,B重合),作CD∥y轴交直线l2于点D,过点C,D分别向y轴作垂线,垂足分别为F,E,得到矩形CDEF.
①设点C的纵坐标为a,求点D的坐标(用含a的代数式表示);
②若矩形CDEF的面积为60,请直接写出此时点C的坐标.
【答案】(1)l1的表达式为y=![]() x,l2的表达式为=-x+24,(2) ①D(3a, -3a+24)②C(3, 1) 或C(15, 5)
x,l2的表达式为=-x+24,(2) ①D(3a, -3a+24)②C(3, 1) 或C(15, 5)
【解析】解:(1)设直线l1的表达式为y=k1x,∵直线l1过B(18, 6),∴18k1=6 ,即k1=![]() 。
。
∴直线l1的表达式为y=![]() x。
x。
设直线l2的表达式为y=k2x+b,∵直线l2过A (0, 24), B(18, 6),
∴![]() 解得
解得![]()
y∴直线l2的表达式为=-x+24。

(2) ①∵点C在直线l1上, 且点C的纵坐标为a,
∴a=![]() x,得x=3a。 ∴点C的坐标为 (3a, a)。
x,得x=3a。 ∴点C的坐标为 (3a, a)。
∵CD∥y轴,∴点D的横坐标为3a 。
∵点D在直线l2上 ,∴y=-3a+24。∴D(3a, -3a+24)。
②C(3, 1) 或C(15, 5)。
(1)设直线l1的表达式为y=k1x,它过(18,6)可求出k1的值,从而得出其解析式;设直线l2的表达式为y=k2+b,由于它过点A(0,24),B(18,6),故把此两点坐标代入即可求出k2,b的值,从而得出其解析式。
(2)①因为点C在直线l1上,且点C的纵坐标为a,故把y=a代入直线l1的表达式即可得出x的值,从而得出C点坐标;由于CD∥y轴,所以点D的横坐标为3a,再根据点D在直线l2上即可得出点D的纵坐标,从而得出结论。
②先根据C、D两点的坐标用a表示出CF及CD的值,由矩形的面积为60即可求出a的值,得出C点坐标:
∵C(3a,a),D(3a,-3a+24),∴CF=3a,CD=-3a+24-a=-4a+24。
∵矩形CDEF的面积为60,∴S矩形CDEF=CFCD=3a×(-4a+24)=60,解得a=1或a=5
当a=1是,3a=3,故C(3,1);当a=5时,3a=15,故C(15,5)。
综上所述C点坐标为:C(3,1)或C(15,5)。


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】计算(x+y)2m·(y+x)3·(x+y)2n+2的结果是( )
A. (x+y)2m+2n+5 B. (x+y)2m+2n+6 C. (x+y)6m+2(n+1) D. -(x+y)2m+2n+5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方. 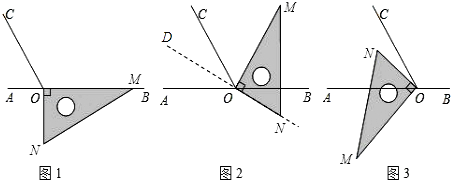
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“五一”期间举行促销活动,根据顾客按商品标价一次性购物总额,规定相应的优惠方法:①如果不超过500元,则不予优惠;②如果超过500元,但不超过800元,则按购物总额给予8折优惠;③如果超过800元,则其中800元给予8折优惠,超过800元的部分给予6折优惠.促销期间,小红和她母亲分别看中一件商品,若各自单独付款,则应分别付款480元和520元;若合并付款,则她们总共只需付款元.
查看答案和解析>>
科目:初中数学 来源: 题型:
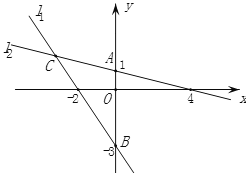
【题目】两个一次函数的图象如图所示,
(1)分别求出两个一次函数的解析式;
(2)求出两个一次函数图象的交点C坐标;
(3)求这两条直线与y轴围成△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级学生小聪和小明完成了数学实验《钟面上的数学》之后,自制了一个模拟钟面,如图所示,O为模拟钟面圆心,M、O、N在一条直线上,指针OA、OB分别从OM、ON出发绕点O转动,OA运动速度为每秒15°,OB运动速度为每秒5°,当一根指针与起始位置重合时,运动停止,设转动的时间为t秒,请你试着解决他们提出的下列问题: 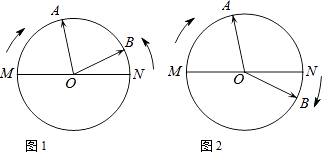
(1)若OA顺时针转动,OB逆时针转动,t=秒时,OA与OB第一次重合;
(2)若它们同时顺时针转动,
①当 t=2秒时,∠AOB=°;
②当t为何值时,OA与OB第一次重合?
③当t为何值时,∠AOB=30°?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知不等式组 ![]() 的整数解为1、2、3,如果把适合这个不等式组的整数a、b组成有序数对(a,b),那么对应在平面直角坐标系上的点共有的个数为 .
的整数解为1、2、3,如果把适合这个不等式组的整数a、b组成有序数对(a,b),那么对应在平面直角坐标系上的点共有的个数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2 , 点A是l1上的动点,点B在l1上,点C、D在l2上,∠ABC,∠ADC的平分线交于点E(不与点B,D重合).
(1)若点A在点B的左侧,∠ABC=80°,∠ADC=60°,过点E作EF∥l1 , 如图①所示,求∠BED的度数. 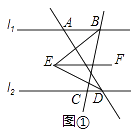
(2)若点A在点B的左侧,∠ABC=α°,∠ADC=60°,如图②所示,求∠BED的度数;(直接写出计算的结果) 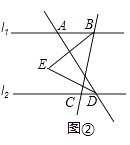
(3)若点A在点B的右侧,∠ABC=α°,∠ADC=60°,如图③所示,求∠BED的度数. 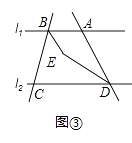
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com