
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方. 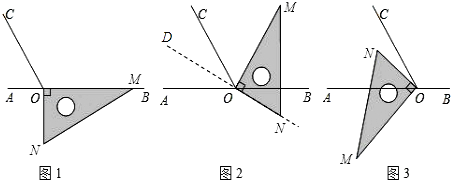
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.
【答案】
(1)解:直线ON平分∠AOC.
理由如下:
如图,设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB= ![]() ,
,
又∠MOD=∠MON=90°,
∴∠COD=90°﹣∠BOC=30°,
∵∠AOC=180°﹣∠BOC=60°,
∴∠COD= ![]() ∠AOC,
∠AOC,
∴OD平分∠AOC,
即直线ON平分∠AOC
(2)解:∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON,∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°.
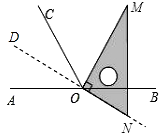
【解析】(1)设ON的反向延长线为OD,由旋转的性质可知∠M=30°,∠MNO=60°,从而可分别求得∠BON=∠AOD=∠COD=30°;(2)分别用∠AON表示出∠AOM和∠NOC即可.
【考点精析】通过灵活运用旋转的性质,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.


科目:初中数学 来源: 题型:
【题目】体育文化用品商店购进篮球和排球共20个,进价和售价如表,全部销售完后共获利润260元.
篮球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(1)购进篮球和排球各多少个?
(2)销售6个排球的利润与销售几个篮球的利润相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空
依据下列解方程 ![]() 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
解:去分母,得3(3x+5)=2(2x﹣1).()
去括号,得9x+15=4x﹣2()
(),得9x﹣4x=﹣15﹣2.()
合并,得5x=﹣17()
(),得 ![]() .()
.()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-x5·x2·x10;
(2)(-2)9×(-2)8×(-2)3;
(3)a6·a2+a5·a3-2a·a7;
(4)(-a)2·(-a)3·a6.
查看答案和解析>>
科目:初中数学 来源: 题型:
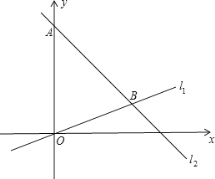
【题目】已知,如图,在平面直角坐标系内,点A的坐标为(0,24 ),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
(1)求直线l1,l2的表达式;
(2)点C为线段OB上一动点 (点C不与点O,B重合),作CD∥y轴交直线l2于点D,过点C,D分别向y轴作垂线,垂足分别为F,E,得到矩形CDEF.
①设点C的纵坐标为a,求点D的坐标(用含a的代数式表示);
②若矩形CDEF的面积为60,请直接写出此时点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com