练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

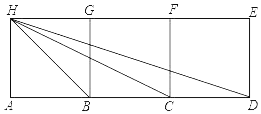
    【题目】如图，四边形ABGH、BCFG、CDEF是边长为1的正方形，连接BH、CH、DH，求证：∠ABH+∠ACH+∠ADH＝90°．

    【答案】见解析

    【解析】

    由四边形ABGH，四边形BCFG，四边形CDEF都是正方形，易得＝＝ ，继而可证得△HBC∽△DBH，然后有相似三角形对应角相等，求得∠ACH＝∠DHB，再利用三角形外角的性质求解即可求得答案．

    证明：∵四边形ABGH，四边形BCFG，四边形CDEF都是正方形，设边长为a，

    则BH＝ ＝a，BC＝a，BD＝2a，

    ∴＝＝，

    又∵∠HBC＝∠DBH（公共角），

    ∴△HBC∽△DBH，

    ∴∠ACH＝∠DHB，

    ∴∠ACH+∠ADH＝∠DHB+∠ADH＝∠ABH＝45°，

    ∵∠ABH＝45°，

    ∴∠ABH+∠ACH+∠ADH＝90°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

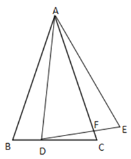
    【题目】如图，已知在△ABC中，AB=AC，点D为BC上一点（不与点B、点C重合），连结AD，以AD为边在AC同侧作△ADE，DE交AC于点F，其中AD=AE，∠ADE=∠B.

    （1）求证：△ABD∽△AEF；

    （2）若，记△ABD的面积为S1，△AEF的面积为S2，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

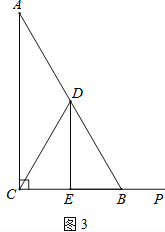
    【题目】在Rt△ABC中，∠ACB=90°，∠A=30°，点D是AB的中点，DE⊥BC，垂足为点E，连接CD．

    （1）如图1，DE与BC的数量关系是　 　；

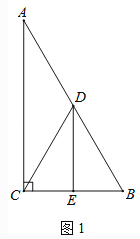
    （2）如图2，若P是线段CB上一动点（点P不与点B、C重合），连接DP，将线段DP绕点D逆时针旋转60°，得到线段DF，连接BF，请猜想DE、BF、BP三者之间的数量关系，并证明你的结论；

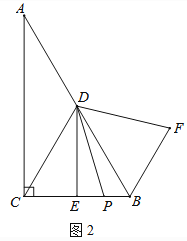
    （3）若点P是线段CB延长线上一动点，按照（2）中的作法，请在图3中补全图形，并直接写出DE、BF、BP三者之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

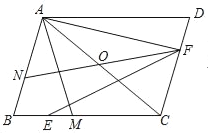
    【题目】如图，平行四边形ABCD中，点O是对角线AC的中点，点M为BC上一点，连接AM，且AB=AM，点E为BM中点，AF⊥AB，连接EF，延长FO交AB于点N．

    （1）若BM=4，MC=3，AC=，求AM的长度；

    （2）若∠ACB=45°，求证：AN+AF=EF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

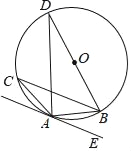
    【题目】如图，BD为△ABC外接圆⊙O的直径，且∠BAE＝∠C．

    （1）求证：AE与⊙O相切于点A；

    （2）若AE∥BC，BC＝2，AC＝2，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现如今，“垃圾分类”意识已深入人心，垃圾一般可分为：可回收物、厨余垃圾、有害垃圾、其它垃圾．其中甲拿了一袋垃圾，乙拿了两袋垃圾．

    （1）直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率；

    （2）求乙所拿的两袋垃圾不同类的概率.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某医药厂两年前生产1t某种药品的成本是5000元，随着生产技术的进步，现在生产1t该种药品的成本是3000元．设该种药品生产成本的年平均下降率为x，则下列所列方程正确的是（　　）

    A. 5000×2（1﹣x）=3000 B. 5000×（1﹣x）2=3000

    C. 5000×（1﹣2x）=3000 D. 5000×（1﹣x2）=3000

    查看答案和解析>>

    科目：初中数学 来源： 题型：

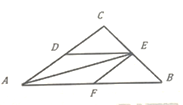
    【题目】如图，在△ABC中，AB=3+,∠B=45°，∠C=105°，点 D、E、F分别在AC、BC、AB上，且四边形ADEF为菱形，若点P是AE上一个动点，则PF+PB的最小值为___________ 。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，BD平分∠ABC，∠BAD=∠BDC=90°，E为BC的中点，AE与BD相交于点F．若BC=4，∠CBD=30°，则DF的长为（　　）

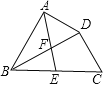
    A. B. C. D.

    查看答案和解析>>

    同步练习册答案