
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
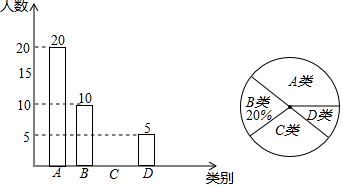
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一抛物线型的立交桥桥拱,这个桥拱的最大高度为16米,跨度为40米,若要在跨度中心点M的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?
如图,有一抛物线型的立交桥桥拱,这个桥拱的最大高度为16米,跨度为40米,若要在跨度中心点M的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
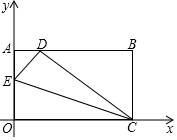 如图,有一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10,如图,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点处,则点E的坐标为(0,$\frac{10}{3}$).
如图,有一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10,如图,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点处,则点E的坐标为(0,$\frac{10}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
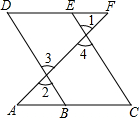 推理填空:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
推理填空:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com