
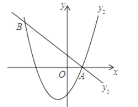
【题目】如图,一次函数y1=kx+1与二次函数y2=ax2+bx﹣2交于A,B两点,且A(1,0)抛物线的对称轴是x=﹣![]() .
.
(1)求k和a、b的值;
(2)求不等式kx+1>ax2+bx﹣2的解集.
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
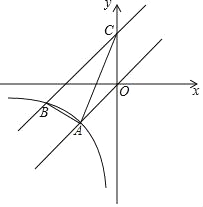
【题目】已知:如图,在平面直角坐标系中,正比例函数y=x的图象与反比例函数y=![]() (k≠0)的图象交于点A(﹣2,﹣2),其中将直线OA向上平移3个单位后与y轴交于点C,与反比例函数在第三象限内交点为B(﹣4,m).
(k≠0)的图象交于点A(﹣2,﹣2),其中将直线OA向上平移3个单位后与y轴交于点C,与反比例函数在第三象限内交点为B(﹣4,m).
(1)求该反比例函数的解析式与平移后的直线解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,运载火箭从地面L处垂直向上发射,当火箭到达A点时,从位于地面R处的雷达测得AR的距离是40km,仰角是30°,n秒后,火箭到达B点,此时仰角是45°,则火箭在这n秒中上升的高度是_____km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴,并在所给坐标系中画出该函数的图象;
(3)该函数的图象经过怎样的平移得到y=x2的图象?
查看答案和解析>>
科目:初中数学 来源: 题型:
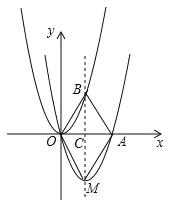
【题目】如图,在平面直角坐标系中,抛物线y1=ax(x﹣2)与x轴交于O、A两点,顶点为M,对称轴BM交抛物线![]() 于点B,交x轴于点C,连接OB、AB、OM、AM,已知0<a<4,四边形OMAB的面积为S.
于点B,交x轴于点C,连接OB、AB、OM、AM,已知0<a<4,四边形OMAB的面积为S.
特例探究:填表:

归纳证明:
当a=2时,证明四边形OMAB是菱形;
拓展应用
(1)将抛物线y1=ax(x﹣2)改为抛物线y3=ax(x﹣2m)(m>0),其他条件不变,当四边形OMAB为正方形时,a= ,m= .
(2)将抛物线y1=ax(x﹣2)改为抛物线y3=ax(x﹣2m)(m>0),其他条件不变,S= (用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017辽宁省盘锦市,第18题,3分)如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线![]() 于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线
于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线![]() 于点B3,…,按照此规律进行下去,则点An的横坐标为______.
于点B3,…,按照此规律进行下去,则点An的横坐标为______.
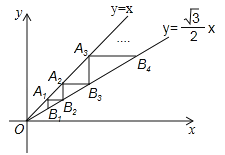
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() (其中
(其中![]() 为常数,
为常数,![]() ),
),![]() 取不同数值时,可得不同直线,请研究这些直线的共同特征.
取不同数值时,可得不同直线,请研究这些直线的共同特征.
实践操作
(1)当![]() 时,直线
时,直线![]() 的解析式为________,请在图1中画出图象.
的解析式为________,请在图1中画出图象.
当![]() 时,直线
时,直线![]() 的解析式为________,请在图2中画出图象
的解析式为________,请在图2中画出图象
(2)探索发现:
直线![]() 必经过点(_______,_______).
必经过点(_______,_______).
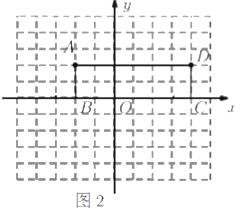
(3)类比迁移:
矩形![]() 如图2所示,若直线
如图2所示,若直线![]() 分矩形
分矩形![]() 的面积为相等的两部分,请在图中直接画出这条直线.
的面积为相等的两部分,请在图中直接画出这条直线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com