
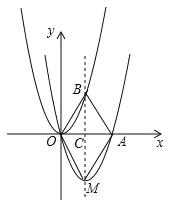
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy1ЃНaxЃЈxЉ2ЃЉгыxжсНЛгкOЁЂAСНЕуЃЌЖЅЕуЮЊMЃЌЖдГЦжсBMНЛХзЮяЯп![]() гкЕуBЃЌНЛxжсгкЕуCЃЌСЌНгOBЁЂABЁЂOMЁЂAMЃЌвбжЊ0ЃМaЃМ4ЃЌЫФБпаЮOMABЕФУцЛ§ЮЊSЃЎ
гкЕуBЃЌНЛxжсгкЕуCЃЌСЌНгOBЁЂABЁЂOMЁЂAMЃЌвбжЊ0ЃМaЃМ4ЃЌЫФБпаЮOMABЕФУцЛ§ЮЊSЃЎ
ЬиР§ЬНОПЃКЬюБэЃК

ЙщФЩжЄУїЃК
ЕБaЃН2ЪБЃЌжЄУїЫФБпаЮOMABЪЧСтаЮЃЛ
ЭиеЙгІгУ
ЃЈ1ЃЉНЋХзЮяЯпy1ЃНaxЃЈxЉ2ЃЉИФЮЊХзЮяЯпy3ЃНaxЃЈxЉ2mЃЉЃЈmЃО0ЃЉЃЌЦфЫћЬѕМўВЛБфЃЌЕБЫФБпаЮOMABЮЊе§ЗНаЮЪБЃЌaЃНЁЁ ЁЁЃЌmЃНЁЁ ЁЁЃЎ
ЃЈ2ЃЉНЋХзЮяЯпy1ЃНaxЃЈxЉ2ЃЉИФЮЊХзЮяЯпy3ЃНaxЃЈxЉ2mЃЉЃЈmЃО0ЃЉЃЌЦфЫћЬѕМўВЛБфЃЌSЃНЁЁ ЁЁЃЈгУКЌmЕФДњЪ§ЪНБэЪОЃЉЃЎ
ЁОД№АИЁПЬиР§ЬНОПЃК4ЃЌ4ЃЌ4ЃЛЙщФЩжЄУїЃКД№АИМћНтЮіЃЛЭиеЙгІгУЃКЃЈ1ЃЉ2ЃЌ![]() ЃЛЃЈ2ЃЉ4m3ЃЎ
ЃЛЃЈ2ЃЉ4m3ЃЎ
ЁОНтЮіЁП
ЬиР§ЬНОПЃКИљОнЬтвтПЩЕУЕуAЕФзјБъЃЌЗжБ№ЧѓЕУЕБaЕФжЕЗжБ№ШЁ1ЃЌ2ЃЌ3ЪБЃЌBгыMЕФзјБъЃЌМДПЩЧѓЕУД№АИЃЛ
ЙщФЩжЄУїЃКгЩХзЮяЯпy=axЃЈx-2ЃЉЃЈ0ЃМaЃМ4ЃЉгыxжсНЛгкOЃЌAСНЕуЃЌПЩЧѓЕУЕуAЕФзјБъЃЌЧѓЕУЖдГЦжсЃЌдђПЩЧѓЕУЕуMгыЕуBЕФзјБъЃЌМДПЩжЄЕУНсТлЃЛ
ЭиеЙгІгУ
ЃЈ1ЃЉгЩХзЮяЯпy=axЃЈx-2mЃЉЃЈ0ЃМaЃМ4ЃЉгыxжсНЛгкOЃЌAСНЕуЃЌЪзЯШПЩЧѓЕУЕуAЕФзјБъЃЌдйЧѓЕУЖдГЦжсЃЌдђПЩЧѓЕУЕуMгыЕуBЕФзјБъЃЌгЩЫФБпаЮOMABЮЊе§ЗНаЮЃЌПЩЕУЗНГЬзщ![]() ЃЌДгЖјЧѓЕУД№АИЃЛ
ЃЌДгЖјЧѓЕУД№АИЃЛ
ЃЈ2ЃЉНсКЯЙщФЩжЄУїгыЃЈ1ЃЉЃЌМДПЩЧѓЕУД№АИЃЎ
ЬиР§ЬНОПЃКЕБy1ЃН0ЪБЃЌaxЃЈxЉ2ЃЉЃН0ЃЌНтЕУЃКx1ЃН0ЃЌx2ЃН2ЃЌЁрЕуAЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌЁрХзЮяЯпy1ЃНaxЃЈxЉ2ЃЉЕФЖдГЦжсЮЊжБЯпxЃН1ЃЎ
ЕБxЃН1ЪБЃЌy1ЃНaxЃЈxЉ2ЃЉЃНЉaЃЌЁрЕуMЕФзјБъЮЊЃЈ1ЃЌЉaЃЉЃЌ
ЕБxЃН1ЪБЃЌy2ЃНЃЈ4ЉaЃЉx2ЃН4ЉaЃЌЁрЕуBЕФзјБъЮЊЃЈ1ЃЌ4ЉaЃЉЃЌ
ЁрOAЃН2ЃЌBMЃН4ЉaЉЃЈЉaЃЉЃН4ЃЌЁрSЃНSЁїOAB+SЁїOAMЃН![]() OABMЃН
OABMЃН![]() ЁС2ЁС4ЃН4ЃЎ
ЁС2ЁС4ЃН4ЃЎ
ЙЪД№АИЮЊЃК4ЃЛ4ЃЛ4ЃЎ
ЙщФЩжЄУїЃКЕБaЃН2ЪБЃЌЕуMЕФзјБъЮЊЃЈ1ЃЌЉ2ЃЉЃЌЕуBЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЌЁрBCЃНCMЃЎ
ЁпЕуAЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌХзЮяЯпy1ЃНaxЃЈxЉ2ЃЉЕФЖдГЦжсЮЊжБЯпxЃН1ЃЎЁрOCЃНAC.
ЁрЫФБпаЮOMABЪЧЦНааЫФБпаЮ
ЁпBMЁЭOAЃЌЁрЕБaЃН2ЪБЃЌЫФБпаЮOMABЪЧСтаЮЃЛ
ЭиеЙгІгУЃКЃЈ1ЃЉЕБy3ЃН0ЪБЃЌaxЃЈxЉ2mЃЉЃН0ЃЌНтЕУЃКx1ЃН0ЃЌx2ЃН2mЃЌЁрЕуAЕФзјБъЮЊЃЈ2mЃЌ0ЃЉЃЌЁрХзЮяЯпy3ЃНaxЃЈxЉ2mЃЉЕФЖдГЦжсЮЊжБЯпxЃНmЃЎ
ЕБxЃНmЪБЃЌy3ЃНaxЃЈxЉ2mЃЉЃНЉam2ЃЌЁрЕуMЕФзјБъЮЊЃЈmЃЌЉam2ЃЉЃЌ
ЕБxЃНmЪБЃЌy2ЃНЃЈ4ЉaЃЉx2ЃНЃЈ4ЉaЃЉm2ЃЌЁрЕуBЕФзјБъЮЊЃЈmЃЌЃЈ4ЉaЃЉm2ЃЉЃЎ
ЁпЫФБпаЮOMABЮЊе§ЗНаЮЃЌЁрBCЃНCMЃНOCЃЌМД![]() ЃЌ
ЃЌ
НтЕУЃКaЃН2ЃЌmЃН![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК2ЃЛ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩжЊЃКOAЃН2mЃЌBMЃНЃЈ4ЉaЃЉm2ЉЃЈЉam2ЃЉЃН4m2ЃЌЁрSЃНSЁїOAB+SЁїOAMЃН![]() OABMЃН
OABMЃН![]() ЁС2mЁС4m2ЃН4m3ЃЎ
ЁС2mЁС4m2ЃН4m3ЃЎ
ЙЪД№АИЮЊЃК4m3ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФВПЗжЭМЯѓШчЭМЃЌЭМЯѓЙ§ЕуЃЈЉ1ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯпxЃН2ЃЌЯТСаНсТлЃКЂйabcЃО0ЃЛЂк9a+cЃО3bЃЛЂл8a+7b+2cЃО0ЃЛЂмЕБxЃОЉ1ЪБЃЌyЕФжЕЫцxжЕЕФдіДѓЖјдіДѓЃЎЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉИіЃЎ
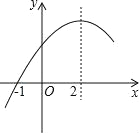
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊе§ЗНаЮDEFGЕФЖЅЕуDЁЂEдкЁїABCЕФБпBCЩЯЃЌЖЅЕуGЁЂFЗжБ№дкБпABЁЂACЩЯЃЎШчЙћBC=4ЃЌЁїABCЕФУцЛ§ЪЧ6ЃЌФЧУДетИіе§ЗНаЮЕФБпГЄЪЧ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
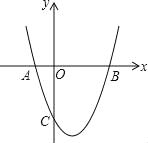
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=![]() +bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкCЃЈ0ЃЌЉ3ЃЉЃЎ
+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкCЃЈ0ЃЌЉ3ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉDЪЧyжсе§АыжсЩЯЕФЕуЃЌOD=3ЃЌдкЯпЖЮBDЩЯШЮШЁвЛЕуEЃЈВЛгыBЃЌDжиКЯЃЉЃЌОЙ§AЃЌBЃЌEШ§ЕуЕФдВНЛжБЯпBCгкЕуFЃЌ
ЂйЪдЫЕУїEFЪЧдВЕФжБОЖЃЛ
ЂкХаЖЯЁїAEFЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЮЊСЫНкдМПЊжЇЃЌЙКТђСЫжЪСПЯрЭЌЕФСНжжбеЩЋЕФВаШБЕизЉЃЌзМБИгУРДзАаоЕиУцЃЌЯжвбМгЙЄГЩШчЭМ1ЫљЪОЕФЕШбќжБНЧШ§НЧаЮЃЌЭѕДЯЭЌбЇЩшМЦСЫШчЭМ2ЫљЪОЕФЫФжжЭМАИЃЎ
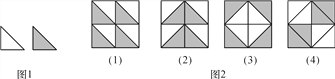
(1)ФуЯВЛЖФФжжЭМАИЃПВЂМђЪіИУЭМАИЕФаЮГЩЙ§ГЬЃЎ
(2)ЧыФуРћгУЫљбЇЙ§ЕФжЊЪЖдйЩшМЦвЛЗљгыЩЯЪіВЛЭЌЕФЭМАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
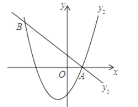
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y1=kx+1гыЖўДЮКЏЪ§y2=ax2+bxЉ2НЛгкAЃЌBСНЕуЃЌЧвAЃЈ1ЃЌ0ЃЉХзЮяЯпЕФЖдГЦжсЪЧx=Љ![]() ЃЎ
ЃЎ
(1)ЧѓkКЭaЁЂbЕФжЕЃЛ
(2)ЧѓВЛЕШЪНkx+1ЃОax2+bxЉ2ЕФНтМЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAЃЌBСНзљГЧЪаЯрОр100ЧЇУзЃЌЯжМЦЛЎвЊдкСНзљГЧЪажЎМфаожўвЛЬѕИпЕШМЖЙЋТЗЃЈМДЯпЖЮABЃЉЁЃОВтСПЃЌЩСжБЃЛЄЧјжааФPЕудкAГЧЪаЕФББЦЋЖЋ30ЁуЗНЯђЃЌBГЧЪаЕФББЦЋЮї45ЁуЗНЯђЩЯЁЃвбжЊЩСжБЃЛЄЧјЕФЗЖЮЇдквдPЮЊдВаФЃЌ50ЧЇУзЮЊАыОЖЕФдВаЮЧјгђФкЃЌЧыЮЪЃКМЦЛЎаожўЕФетЬѕИпЕШМЖЙЋТЗЛсВЛЛсДЉдНБЃЛЄЧјЃПЮЊЪВУДЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОЬтТњЗж8ЗжЃЉ
МзЁЂввСНЭЌбЇгУвЛИБЦЫПЫХЦжаХЦУцЪ§зжЗжБ№ЪЧ3ЁЂ4ЁЂ5ЁЂ6ЕФ4еХХЦзіГщЪ§бЇгЮЯЗЃЎгЮЯЗЙцдђЪЧЃКНЋет4еХХЦЕФе§УцШЋВПГЏЯТЃЌЯДдШЃЌДгжаЫцЛњГщШЁвЛеХЃЌГщЕУЕФЪ§зїЮЊЪЎЮЛЩЯЕФЪ§зжЃЌШЛКѓЃЌНЋЫљГщЕФХЦЗХЛиЃЌе§УцШЋВПГЏЯТЁЂЯДдШЃЌдйДгжаЫцЛњГщШЁвЛеХЃЌГщЕУЕФЪ§зїЮЊИіЮЛЩЯЕФЪ§зжЃЌетбљОЭЕУЕНвЛИіСНЮЛЪ§ЃЎШєетИіСНЮЛЪ§аЁгк45ЃЌдђМзЛёЪЄЃЌЗёдђввЛёЪЄЃЎФуШЯЮЊетИігЮЯЗЙЋЦНТ№ЃПЧыдЫгУИХТЪжЊЪЖЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкОиаЮABCDжаЃЌAB=5ЃЌBC=12ЃЌЕуAдкЁбBЩЯЃЌШчЙћЁбDгыЁбBЯрНЛЃЌЧвЕуBдкЁбDФкЃЌФЧУДЁбDЕФАыОЖГЄПЩвдЕШгк________ЃЎЃЈжЛашаДГівЛИіЗћКЯвЊЧѓЕФЪ§ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com