
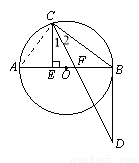
如图,AB是⊙O的直径,点C在⊙O上,CEAB于E,CD平分ECB,交过点B的射线于D,交AB于F,且BC=BD.

(1)求证:BD是⊙O的切线;
(2)若AE=9,CE=12,求BF的长.
(2)BF=10
【解析】
试题分析:(1)根据垂直的定义可得∠CEB=90°,然后根据角平分线的性质和等腰三角形的性质,判断出∠1=∠D,从而根据平行线的判定得到CE∥BD,根据平行线的性质得∠DBA=∠CEB,由此可根据切线的判定得证结果;
(2)连接AC,由射影定理可得 ,进而求得EB的长,再由勾股定理求得BD=BC的长,然后由“两角对应相等的两三角形相似”的性质证得△EFC∽△BFD,再由相似三角形的性质得出结果.
,进而求得EB的长,再由勾股定理求得BD=BC的长,然后由“两角对应相等的两三角形相似”的性质证得△EFC∽△BFD,再由相似三角形的性质得出结果.
试题解析:(1)证明:∵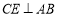 ,
,
∴ 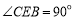 .
.
∵ CD平分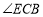 ,BC=BD,
,BC=BD,
∴  ,
, .
.
∴ 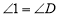 .
.
∴ 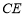 ∥
∥ .
.
∴ 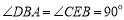 .
.
∵ AB是⊙O的直径,
∴ BD是⊙O的切线.
(2)连接AC,
∵ AB是⊙O直径,
∴ 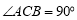 .
.
∵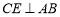 ,
,
可得  .
.
∴ 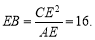
在Rt△CEB中,∠CEB=90,由勾股定理得
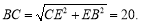
∴  .
.
∵ 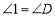 ,∠EFC =∠BFD,
,∠EFC =∠BFD,
∴ △EFC∽△BFD.
∴ 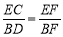 .
.
∴ 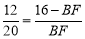 .
.
∴ BF=10.
考点:切线的判定,相似三角形,勾股定理


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源:2014-2015学年广东省梅州市九年级上学期第一次月考数学试卷(解析版) 题型:填空题
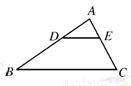
如图,在△ABC中,DE∥BC,AD=5,BD=10,AE=3,则CE的值为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省三门峡市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,直线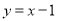 与反比例函数
与反比例函数 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(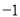 ,m).
,m).
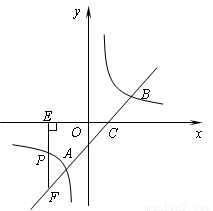
(1)求反比例函数的解析式;
(2)若点P(n,-1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省三门峡市九年级上学期期末考试数学试卷(解析版) 题型:填空题
两圆的圆心距d=6,两圆的半径长分别是方程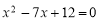 的两根,则这两个圆的位置关系是 .
的两根,则这两个圆的位置关系是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市房山区九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,在△ABC中,D、E分别是AB、AC边上的点,且 DE∥BC,若AD=5,DB=3,DE=4,则BC等于 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com