
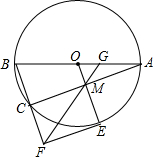
 如图,⊙O是△ABC的外接圆,AB为直径,过点O作OM∥BC,交AC于点M.
如图,⊙O是△ABC的外接圆,AB为直径,过点O作OM∥BC,交AC于点M.分析 (1)根据两直线平行同位角相等即可解决问题.
(2)①先证明四边形CFEM是平行四边形,再证明有一个角为90°即可.
②连接AE,只要证明OG=OM,即可得到EM=AG,即可解决问题.
解答 解:(1)∵AB为直径,
∴∠BCA=90°,
∵OM∥BC,
∴∠AMO=∠BCA=90°.
(2)①四边形CMEF为矩形,理由如下:
∵EF与⊙O相切于点E,
∴∠OEF=90°,
∵∠OMA=∠OMC=∠OEF=90°,
∴EF∥MC,
∵OM∥BC,
∴EM∥FC,
∴四边形CMEF为平行四边形,
∵∠OEF=90°,
∴四边形CMEF为矩形.
②解:连接AE,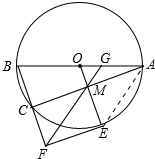
∵O为AB的中点,OM∥BC
∴M为AC的中点,即有CM=AM,
∵四边形CMEF是矩形,
∴AM=CM=EF,
又∵AC∥EF,
∴AMFE为平行四边形,
∴FM∥AE,即GM∥AE,
∴∠OMG=∠OEA,∠OGM=∠OAE
∵OE=OA
∴∠OEA=∠OAE,
∴∠OMG=∠OGM,
∴OM=OG
∵OE=OM+ME=OA=OG+GA,
∴ME=GA=2,
∴矩形CMEF的面积为:CM×ME=3×2=6.
点评 本题考查圆的有关知识、等腰三角形的判定好性质、矩形的判定和性质、平行四边形的判定和性质等知识,解题的关键是平行四边形AEFM的发现,需要灵活应用这些知识,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=-x2+2x+m
已知二次函数y=-x2+2x+m查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com