练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
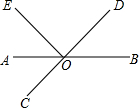
    7．如图，直线AB、CD交于点O，OA平分∠EOC，∠EOC=70°，则∠BOD的度数是（　　）
    A．20°B．30°C．35°D．55°

    分析 首先根据角平分线的定义可知；∠AOC=35°，然后由对顶角的性质可知∠BOD=35°．

    解答 解：∵OA平分∠EOC，
    ∴∠AOC=$\frac{1}{2}∠EOC=\frac{1}{2}×70=35°$．
    由对顶角相等可知：
    ∠BOD=∠AOC=35°．
    故选：C．

    点评 本题主要考查的是对顶角的性质和角平分线的定义，掌握对顶角的性质和角平分线的定义是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

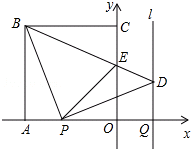    17．如图，正方形OABC的边OA，OC在坐标轴上，点B的坐标为（-3，3）．点P从点A出发，以每秒1个单位长度的速度沿x轴向点O运动；点Q从点O同时出发，以相同的速度沿x轴的正方向运动，规定点P到达点O时，点Q也停止运动．连接BP，过P点作BP的垂线，与过点Q平行于y轴的直线l相交于点D．BD与y轴交于点E，连接PE．设点P运动的时间为t（s）．
    （1）求∠EBP的度数；
    （2）求点D运动路径的长；
    （3）探索△POE周长是否随时间t的变化而变化？若变化，说明理由；若不变，试求这个定值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图是金昌市在“四城”联创活动中制作的一个正方体宣传品的展开图，将它折叠成正方体后“创”字的对面是（　　）
    A．文B．明C．城D．市

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算
    （1）2$\sqrt{12}$+4$\sqrt{\frac{1}{8}}$-3$\sqrt{48}$
    （2）（8$\sqrt{3}$-5$\sqrt{6}$）÷2$\sqrt{3}$
    （3）4$\sqrt{24}$×$\frac{\sqrt{6}}{8}$÷3$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

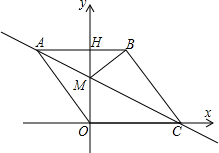    2．如图，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（-3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H，连接BM．
    （1）求直线AC的解析式；
    （2）动点P从点A出发，沿折线ABC的方向以2个单位/秒的速度向终点C匀速运动，设△PMB的面积为S，点P的运动时间为t秒，求S与t之间的函数关系式（要求写出自变量t的取值范围）；
    （3）动点P从点A出发，沿线段AB方向以2个单位/秒的速度向终点B匀速运动，当∠MPB与∠BCO互为余角时，试确定t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．武汉东湖高新开发区某企业新增了一个项目，为了节约资源，保护环境，该企业决定购买A、B两种型号的污水处理设备共8台，具体情况如下表：
    A型B型
    价格（万元/台）1210
    月污水处理能力（吨/月）200160
    经预算，企业最多支出89万元购买设备，且要求月处理污水能力不低于1380吨．设购买A种型号的污水处理设备x台，可列不等式组$\left\{\begin{array}{l}{12x+10（8-x）≤89}\\{200x+160（8-x）≥1380}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．直线y=-2x+1经过的象限是（　　）
    A．三、二、一B．三、四、一C．二、三、四D．二、一、四

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

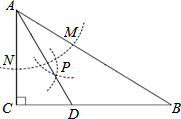    16．如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法①AD是∠BAC的平分线；②∠ADC=60°；③点D在AB的中垂线上；正确的个数是3 个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．如图，△ABC中，BC=a．
    （1）若AD1=$\frac{1}{3}$AB，AE1=$\frac{1}{3}$AC，则D1E1=$\frac{1}{3}$a；
    （2）若D1D2=$\frac{1}{3}$D1B，E1E2=$\frac{1}{3}$E1C，则D2E2=$\frac{5}{9}$a；
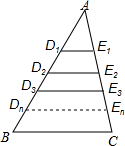    （3）若D2D3=$\frac{1}{3}$D2B，E2E3=$\frac{1}{3}$E2C，则D3E3=$\frac{19}{29}$a．

    查看答案和解析>>

    同步练习册答案