
【题目】在△ABC中,AB=BC,∠ABC=90°.以AB为斜边作等腰直角三角形ADB.点P是直线DB上一个动点,连接AP,作PE⊥AP交BC所在的直线于点E.

(1)如图1,点P在BD的延长线上,PE⊥EC,AD=1,直接写出PE的长;
(2)点P在线段BD上(不与B,D重合),依题意,将图2补全,求证:PA=PE;
(3)点P在DB的延长线上,依题意,将图3补全,并判断PA=PE是否仍然成立.
【答案】(1)![]() ; (2)证明见解析;(3)证明见解析.
; (2)证明见解析;(3)证明见解析.
【解析】
(1)根据等腰直角三角形的性质得到∠ABP=45°,根据勾股定理得到AB=![]() =
=![]() ,推出四边形ABEP是矩形,得到四边形ABEP是正方形,于是得到结论;(2)根据等腰直角三角形的性质得到∠ADB=90°,∠DAB=∠DBA=45°,求得∠PBN=45°过P作PM⊥AB于点M,过P作PN⊥BC于点N,于是得到PM=PN,∠BPN=45°根据全等三角形的性质即可得到结论;
,推出四边形ABEP是矩形,得到四边形ABEP是正方形,于是得到结论;(2)根据等腰直角三角形的性质得到∠ADB=90°,∠DAB=∠DBA=45°,求得∠PBN=45°过P作PM⊥AB于点M,过P作PN⊥BC于点N,于是得到PM=PN,∠BPN=45°根据全等三角形的性质即可得到结论;
(3)根据等腰直角三角形的性质得到∠ABD=45°,得到∠PBN=45°,∠ABC=90°,过P作PM⊥AB于点M,过P作PN⊥BC于点N,得到四边形BMPN是矩形,推出四边形BMPN是正方形,得到PM=PN,根据全等三角形的性质即可得到结论.
(1)∵AD=DB=1,∠ADB=90°,
∴∠ABP=45°,AB=![]() =
=![]() ,
,
∵PE⊥AP,AB⊥BC,
∴PA∥EC,
∴PA⊥AB,
∴四边形ABEP是矩形,
∵∠ABP=45°,
∴PA=AB,
∴四边形ABEP是正方形,
∴PE=AB=![]()
(2)∵△ABC和△ADB是等腰直角三角形,
∴∠ADB=90°,∠DAB=∠DBA=45°,
∴∠PBN=45°
∴PE⊥AP,∠DAP=∠BPE=90°-∠DPA,
∵∠PAM=45°-∠DAP,∠PEN=45°-∠BPE,
∴∠PAM=∠PEN,
过P作PM⊥AB于点M,过P作PN⊥BC于点N,

则PM=PN,∠BPN=45°,
在△APM和△EPN中,
 ,
,
∴△APM≌△EPN,
∴PA=PE;
(3)∵△ABC和△ADB是等腰直角三角形,
∴∠ABD=45°,
∴∠PBN=45°,∠ABC=90°,
过P作PM⊥AB于点M,过P作PN⊥BC于点N,

则四边形BMPN是矩形,
∵∠NBP=45°,
∴四边形BMPN是正方形,
∴PM=PN,
∵AB⊥BC,
∴∠BAN=∠APN,
∵AP⊥PE,
∴∠APN=∠E,
∴∠BAP=∠E,
在△AMP与△ENP中,
 ,
,
∴△AMP≌△ENP,
∴AP=PE.


科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字﹣2,﹣1,1,4的小球,它们的形状、大小、质地等完全相同,小强先从盒子里随机取出一个小球,记下数字为a;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为b.
(1)用列表法或画树状图表示出(a,b)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(a,b)落在二次函数y=x2的图象上的概率;
(3)求小强、小华各取一次小球所确定的数a,b满足直线y=ax+b经过一、二、三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
A.![]()
B.![]()
C.4
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作角的平分线”的尺规作图的过程.
已知:如图1,![]() .
.
求作:射线![]() ,使它平分
,使它平分![]() .
.
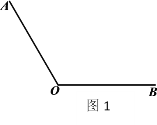
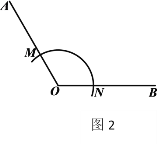
作法:如图2,
①以点![]() 为圆心,任意长为半径作弧,交
为圆心,任意长为半径作弧,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ;
;
②分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的同样长为半径作弧,两弧交于点
的同样长为半径作弧,两弧交于点![]() ;
;
③作射线![]() .
.
所以射线![]() 就是所求作的射线.
就是所求作的射线.
根据小明设计的尺规作图的过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,
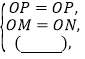
∴![]() ≌
≌![]() ( )(填推理的依据).
( )(填推理的依据).
∴ (全等三角形的 相等).
即射线![]() 平分
平分![]() (角平分线定义).
(角平分线定义).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来数的情况下,为估计白球数,小刚向其中放入8个黑球摇匀后,从中随意摸出一个球记下颜色,再把它放回盒中,不断重复这一过程,共摸球100次,其中20次摸到黑球,你估计盒中大约有白球( )
A.20个
B.28个
C.36个
D.32个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,若以A为旋转中心,将其按顺时针方向旋转60°到△AB'C'位置,则B点经过的路线长为( )
A.π
B.![]()
![]() π
π
C.![]() π
π
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下面的问题:
(1)如果a2+a=3,求a2+a+2015的值.
(2)已知a﹣b=﹣3,求3(b﹣a)2﹣5a+5b+5的值.
(3)已知a2+2ab=﹣3,ab﹣b2=﹣5,求4a2+![]() ab+
ab+![]() b2的值.
b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给的信息解答下列问题:
(1)这次评价中,一共抽查了名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com