
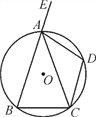
【题目】如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,D为弧AC的中点,E是BA延长线上一点,∠DAE=105°.
(1)求∠CAD的度数;
(2)若⊙O的半径为3,求弧BC的长.
【答案】(1) 35°;(2) ![]() .
.
【解析】
(1)由已知易得![]() ,由此可得∠ACB=2∠ACD,由∠DAE=105°,四边形ABCD是⊙O的内接四边形易得∠BCD=105°,由此可得3∠ACD=105°,从而可得∠ACD=35°;
,由此可得∠ACB=2∠ACD,由∠DAE=105°,四边形ABCD是⊙O的内接四边形易得∠BCD=105°,由此可得3∠ACD=105°,从而可得∠ACD=35°;
(2)由(1)中结论易得∠ABC=∠ACB=70°,由此可得∠BAC=40°,连接OB、OC,则可得∠BOC=80°,这样由弧长计算公式即可求出![]() 的长度了.
的长度了.
(1)∵AB=AC,
∴![]() ,
,
∵D是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴∠ACB=2∠ACD,
∵四边形ABCD内接于⊙O,
∴∠BCD=∠EAD=105°
∴∠ACB+∠ACD=105°,即3∠ACD=105°,
∴∠CAD=∠ACD=35°
(2)∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠BAC=40°,
连结OB,OC,则∠BOC=2∠BAC =80°,
∴![]() 的长
的长![]() .
.



 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中减掉一个边长为b的小正方形(a>b)把余下的部分再剪拼成一个长方形.
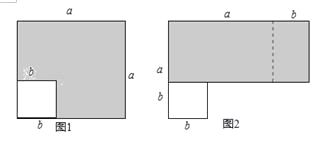
(1)如图1,阴影部分的面积是: ;
(2)如图2,是把图1重新剪拼成的一个长方形,阴影部分的面积是 ;
(3)比较两阴影部分面积,可以得到一个公式是 ;
(4)运用你所得到的公式,计算:99.8×100.2.
查看答案和解析>>
科目:初中数学 来源: 题型:
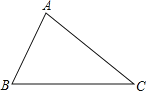
【题目】按要求画图,并解答问题
(1)如图,取BC边的中点D,画射线AD;
(2)分别过点B、C画BE⊥AD于点E,CF⊥AD于点F;
(3)BE和CF的位置关系是 ;通过度量猜想BE和CF的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
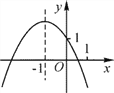
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c>0;②a-b+c>1;③abc>0;④4a-2b+c<1;⑤b+2a=0. 其中所有正确的结论是______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号汽车油箱容量为40L,每行驶100km耗油10L.设一辆加满油的该型号汽车行驶路程为x(km),行驶过程中油箱内剩余油量为y(L)
(1)求y与x之间的函数表达式;
(2)为了有效延长汽车使用寿命,厂家建议每次加油时油箱内剩余油量不低于油箱容量的四分之一,按此建议,求该辆汽车最多行驶的路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com